当前位置：试卷中心 > 试卷详情

2022-2023学年广西桂林十三中八年级（下）期中数学试卷

发布：2024/6/2 8:0:8

1．下列图形中，是中心对称图形的是（　　）
A． B． C． D．
组卷：50引用：4难度：0.9
解析
2．下列四组线段中，可以构成直角三角形的是（　　）
A．1，2，3 B．2，3，4 C．3，4，5 D．4，5，6
组卷：492引用：47难度：0.9
解析
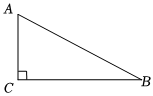3．如图，在△ABC中，∠C=90°，∠B=30°，AB=4．则AC的长度是（　　）
A．3.5 B．3 C．2.5 D．2
组卷：353引用：4难度：0.8
解析
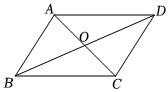4．如图，在平行四边形ABCD中，BC=10，AC=8，BD=14，则△BOC的周长是（　　）
A．10 B．16 C．18 D．21
组卷：116引用：5难度：0.6
解析
5．如图，Rt△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB．若DE=3，BD=6，则BC的长度为（　　）
A．7 B．8 C．9 D．10
组卷：672引用：4难度：0.5
解析
6．下列性质中，平行四边形，矩形，菱形，正方形共有的性质是（　　）
A．对角线相等 B．对角线互相垂直
C．对角线互相平分 D．对角线平分内角
组卷：891引用：14难度：0.9
解析
7．如图，在△ABC中，AB=AC，点D，E分别是BC，AC中点，若∠B=35°，则∠AED=（　　）
A．35° B．50° C．70° D．80°
组卷：263引用：5难度：0.5
解析
8．如图，直角三角形的三边上分别有一个正方形，其中两个正方形的面积分别是25和169，则字母B所代表的正方形的面积是（　　）
A．144 B．194 C．12 D．13
组卷：1710引用：13难度：0.9
解析

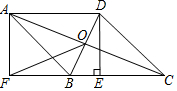25．如图，▱ABCD的对角线AC，BD交于点O，过点D作DE⊥BC于E，延长CB到点F，使BF=CE，连接AF，OF．
（1）求证：四边形AFED是矩形．
（2）若AD=7，BE=2，∠ABF=45°，试求OF的长．
组卷：1822引用：17难度：0.5
解析
26．（1）如图1，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，分别与BA、CD的延长线交于点M、N，证明：∠BME=∠CNE．
请将证明∠BME=∠CNE的过程填写完整：
证明：连接BD，取BD的中点H，连接HE、HF．
∵F是AD的中点，H是BD的中点，
∴HF∥AB，
HF
=
1
2
AB
；同理：HE∥
，HE=
．
∴∠1=∠BME，∠2=∠CNE，
又∵AB=CD，∴HF=HE，∴∠=∠2，∴∠BME=∠CNE．
（2）运用上题方法解决下列问题：
问题一：如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E、F分别是BC、AD的中点，连接EF，分别交DC、AB于点M、N，请判断△OMN的形状，并说明理由；
问题二：如图3，在△ABC中，AC＞AB，点D在AC上，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，与BA的延长线交于G点，若∠EFC=60°，连接GD，判断△AGD的形状并说明理由．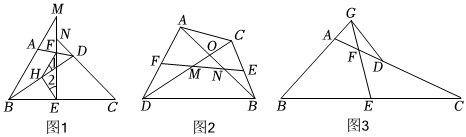
组卷：129引用：1难度：0.2
解析