人教新版九年级上册《第23章 旋转》2023年单元测试卷（13）

一、选择题

• 1．如图是神舟十三号载人飞行任务标识，该标识经过旋转能得到的是（　　）

  A．

  B．

  C．

  D．
  组卷：28引用：1难度：0.7

  解析

• 2．已知点P₁（a,-2）与点P₂（3，b）关于原点对称，则（a+b）²⁰²³=（　　）

  A．-1

  B．1

  C．-52023

  D．52023
  组卷：348引用：11难度：0.9

  解析

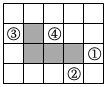• 3．在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（　　）

  A．①

  B．②

  C．③

  D．④
  组卷：375引用：10难度：0.9

  解析

• 4．如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与点A对应，则角α等于（　　）

  A．45°

  B．60°

  C．90°

  D．120°
  组卷：774引用：10难度：0.7

  解析

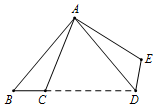• 5．如图，将△ABC绕点A逆时针旋转80°，得到△ADE，若点D在线段BC的延长线上，则∠B的度数为（　　）

  A．40°

  B．45°

  C．50°

  D．55°
  组卷：1296引用：14难度：0.7

  解析

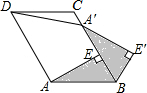• 6．如图，已知在▱ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，AD=5，DC=4，则DA′的大小为（　　）

  A．1

  B． 6

  C． 21

  D．2 3
  组卷：424引用：6难度：0.7

  解析

三、解答题

• 19．阅读与理解：
  图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（点C与点C′重合）的图形．
  操作与证明：
  （1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2，在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
  （2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α（0°≤α≤360°），连接AD，BE，如图3，在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
  猜想与发现：
  根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大，最大是多少？当α为多少度时，线段AD的长度最小，最小是多少？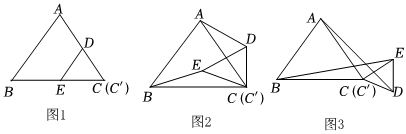
  
  组卷：90引用：9难度：0.1

  解析

• 20．如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连接CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连接QB并延长交直线AD于点E．
  （1）如图1，猜想∠QEP=

  °；
  （2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；
  （3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．
  
  组卷：6044引用：22难度：0.5

  解析