2022-2023学年福建省龙岩市新罗区七年级(下)期末数学试卷
发布:2024/6/29 8:0:10
一、选择题(本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.在下列四个实数-2,-
,0,3中,无理数的是( )227组卷:24引用:2难度:0.8 -
2.下列调查中,适宜采用全面调查的是( )
组卷:16引用:2难度:0.7 -
 3.观察下列图案,能通过如图的图形平移得到的是( )组卷:79引用:2难度:0.9
3.观察下列图案,能通过如图的图形平移得到的是( )组卷:79引用:2难度:0.9 -
 4.有两个不等式的解集在数轴上的表示如图所示,则下列数值是由这两个不等式所组成的不等式组的解的是( )组卷:151引用:2难度:0.8
4.有两个不等式的解集在数轴上的表示如图所示,则下列数值是由这两个不等式所组成的不等式组的解的是( )组卷:151引用:2难度:0.8 -
5.若m>n,下列不等式不一定成立的是( )
组卷:52引用:2难度:0.7 -
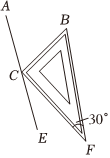 6.一把直尺和一个含30°角的直角三角板按如图所示方式放置.其中三角板的直角顶点C落在直尺AE上,若AE∥BF,则∠BCE的度数为( )组卷:389引用:5难度:0.8
6.一把直尺和一个含30°角的直角三角板按如图所示方式放置.其中三角板的直角顶点C落在直尺AE上,若AE∥BF,则∠BCE的度数为( )组卷:389引用:5难度:0.8 -
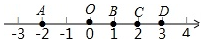 7.如图所示,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示的点P落在线段( )4-5组卷:485引用:4难度:0.8
7.如图所示,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示的点P落在线段( )4-5组卷:485引用:4难度:0.8 -
8.为了节能减排,某公交公司计划购买A型和B型两种新能源公交车.若购买A型公交车1辆,B型公交车2辆,共需270万元;若购买A型公交车2辆,B型公交车1辆,共需300万元,列出方程组
.若对该方程组进行变形可得到方程x-y=30,下列对“x-y=30”的含义说法正确的是( )x+2y=2702x+y=300组卷:69引用:3难度:0.7
三、解答题(本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤)
-
24.(一)阅读材料
若关于x,y的二元一次方程ax+by=c有一组整数解,则方程ax+by=c的全体整数解可表示为x=x0y=y0(t为整数).x=x0+bty=y0-at
例题:求关于x,y的二元一次方程5x+11y=136的所有正整数解.
小明参考阅读材料,解决该例题如下:
解:∵5x+11y=136,∴x=(136-11y)÷5=27-3y+(1+4y)÷5,
∵x,y要取整数,∴当y=1时,x=25,
∴该方程一组整数解为,∴其全体整数解为x0=25y0=1(t为整数).x=25+11ty=1-5t
∵,∴25+11t>01-5t>0.-2511<t<15
∵t为整数,∴t=-2、-1或0.
∴该方程的正整数解为、x=3y=11和x=14y=6.x=25y=1
(二)解决问题
(1)关于x,y的二元一次方程3x+5y=14的全体整数解表示为(t为整数),则a=;x=a+5ty=1-3t
(2)请参考阅读材料,直接写出关于x,y的二元一次方程19x-7y=155的一组整数解和它对应的全体整数解;
(3)请你参考小明的解题方法,求关于x,y的二元一次方程3x+2y=23的全体正整数解.组卷:270引用:3难度:0.4 -
25.如图1,在平面直角坐标系中,A(4,0),B(a,0),C(b,6),且满足(a-b+12)2+|a+b|=0,线段BC交y轴于点D.
(1)求点B、C的坐标;
(2)动点E在y轴上,且在点D的上方,过点E作EF∥BC,作∠ABC、∠OEF的角平分线BP、EP,如图2,求∠BPE的度数;
(3)如图3,若存在坐标轴上的点Q(点Q与A不重合),使得三角形QBC与三角形ABC的面积相等,请直接写出点D坐标和满足条件的点Q坐标.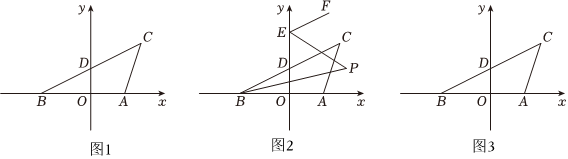 组卷:97引用:1难度:0.1
组卷:97引用:1难度:0.1


