当前位置：试卷中心 > 试卷详情

2021-2022学年江苏省南通市海安实验中学高一（下）期中数学试卷

发布：2024/6/25 8:0:9

一、选择题。本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合U={x|x＜5，x∈N^*}，M={x|x²-5x+4=0}，则∁_UM=（　　）
A．{2，3} B．{1，5} C．{1，4} D．{2，3，5}
组卷：328引用：5难度：0.9
解析
2．已知复数
z
=
3
-
4
i
2
-
i
，则
z
的虚部是（　　）
A．-i B．-1 C．i D．1
组卷：129引用：4难度：0.8
解析
3．在正方体ABCD-A₁B₁C₁D₁中，P为B₁D₁的中点，则直线PB与AC所成的角为（　　）
A．
π
2
B．
π
3
C．
π
4
D．
π
6
组卷：29引用：2难度：0.7
解析
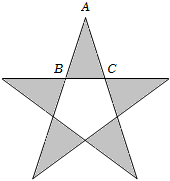4．十七世纪德国著名的天文学家开普勒曾经这样说过“几何学里面有两件宝，一个是勾股定理，一个是黄金分割，如果把勾股定理比作金矿的话，那么可以把黄金分割比作砖石”，黄金三角形有两种，其中底与腰之比为黄金分割比的黄金三角形被认为最美的三角形，它是一个顶角为36°的等腰三角形（另一种是顶角为108°的等腰三角形），如图所示的五角星由五个黄金三角形与一个正五边形组成，在其中一个黄金△ABC中，
BC
AC
=
5
-
1
2
，根据这些信息可得cos36°=（　　）
A．-
5
+
1
4
B．
2
5
-
1
4
C．
5
+
3
8
D．
5
+
1
4
组卷：35引用：3难度：0.6
解析
5．已知向量
e
=
（
3
2
，-
1
2
）
，
a
=
（
3
，
1
）
，则向量
a
在向量
e
上的投影向量为（　　）
A．
-
e
B．
e
C．
a
D．-1
组卷：100引用：4难度：0.8
解析
6．在下列四个正方体中，A、B为正方体的两个顶点，M、N、Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（　　）
A． B． C． D．
组卷：886引用：40难度：0.6
解析
7．设f（x）是定义域为R的奇函数，且f（1+x）=f（-x）．若f（-
1
3
）=
1
3
，则f（
5
3
）=（　　）
A．-
5
3
B．-
1
3
C．
1
3
D．
5
3
组卷：7241引用：44难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题。本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

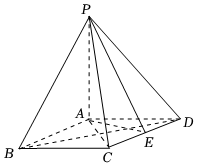21．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底部ABCD为菱形，E为CD的中点．
（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）棱PB上是否存在点F，使得CF∥平面PAE？说明理由．
组卷：50引用：2难度：0.5
解析
22．已知O为坐标原点，对于函数f（x）=asinx+bcosx,称向量
OM
=
（
a
,
b
）
为函数f（x）的相伴特征向量，同时称函数f（x）为向量
OM
的相伴函数．
（1）若
OT
=
（
-
3
，
1
）
为
h
（
x
）
=
msin
（
x
-
π
6
）
的相伴特征向量，求实数m的值；
（2）记向量
ON
=
（
1
，
3
）
的相伴函数为f（x），求当
f
（
x
）
=
8
5
且
x
∈
（
-
π
3
，
π
6
）
时sinx的值；
（3）已知A（-2，3），B（2，6），h（x）为（1）中函数，
φ
（
x
）
=
h
（
x
2
-
π
3
）
，请问在y=φ（x）的图象上是否存在一点P，使得
AP
⊥
BP
，若存在，求出P点坐标；若不存在，说明理由．
组卷：109引用：6难度：0.4
解析