2022-2023学年甘肃省金昌市永昌第一高级中学高二（下）期中数学试卷

一、单项选择题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知函数f（x）=e^x-cosx+1（e为自然对数的底数），则f′（0）等于（　　）

  A．0

  B．1

  C．2

  D．e
  组卷：36引用：1难度：0.9

  解析

• 2．下列四个命题中为真命题的是（　　）

  A．已知A，B，C，D，E是空间任意五点，则 AB + BC + CD + DE + EA =0

  B．若两个非零向量 AB 与 DC 满足 AB = DC ，则四边形ABCD是菱形

  C．若分别表示两个空间向量的有向线段所在的直线是异面直线，则这两个向量可以是共面向量

  D．对于空间的任意一点O和不共线的三点A，B，C，若 OP =x OA +y OB +z OC （x,y,z∈R），则P，A，B，C四点共面
  组卷：215引用：1难度：0.7

  解析

• 3．若直线y=x是函数f（x）=lnx+ax的切线，则实数a的值为（　　）

  A．1

  B．e

  C． 1 - 1 e

  D． 2 - 1 e
  组卷：50引用：1难度：0.6

  解析

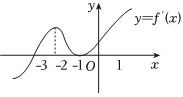• 4．定义在R上的可导函数y=f（x）的导函数的图象如图所示，则以下结论正确的是（　　）

  A．-3是函数f（x）的一个零点

  B．-2是函数f（x）的极大值点

  C．f（x）的单调递增区间是（-3，+∞）

  D．f（x）无最小值
  组卷：55引用：2难度：0.6

  解析

• 5．若

  （

  5

  x

  -

  4

  ）

  2023

  =

  a

  0

  +

  a

  1

  x

  +

  a

  2

  x

  2

  +

  a

  3

  x

  3

  +

  …

  +

  a

  2023

  x

  2023

  （

  x

  ∈

  R

  ）

  ，则（　　）

  A． a 0 = 4 2023

  B． a 1 + a 3 + a 5 + … + a 2023 = 1 - 9 2023 2

  C． a 0 + a 2 + a 4 + … + a 2022 = 1 + 9 2023 2

  D． a 1 5 + a 2 5 2 + a 3 5 3 + … + a 2023 5 2023 = 4 2023 - 3 2023
  组卷：76引用：1难度：0.5

  解析

• 6．若函数f（x）=2ax-lnx在（1，3）上不单调，则实数a的取值范围为（　　）

  A．（2，6）	B．（-∞，2）∪（6，+∞）
  C． （ 1 6 ， 1 2 ）	D． （ - ∞ ， 1 6 ） ∪ （ 1 2 ， + ∞ ）
  组卷：351引用：8难度：0.6

  解析

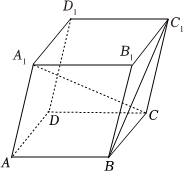• 7．如图，在平行六面体ABCD-A₁B₁C₁D₁中，AB=2，AD=2，AA₁=2，∠BAA₁=∠DAA₁=60°，∠BAD=90°，则BC₁与CA₁所成角的余弦值为（　　）

  A． - 3 6

  B． 3 6

  C． - 2 4

  D． 2 4
  组卷：103引用：2难度：0.6

  解析

四、解答题（本题共6小题，共70分）

• 21．某地规划了一个工业园区，需要架设一条16千米的高压线，已知该段线路两端的高压电线塔已经搭建好，余下的工程只需要在已建好的高压电线塔之间等距离的修建高压电线塔和架设电线．已知一座高压电线塔为2万元，距离为x千米的两相邻高压电线塔之间的电线及人工费等为4x[ln（x+0.48）-0.125]万元，所有电线塔都视为“点”，且不考虑其他因素，记余下的工程费用为y万元．
  （1）试写出y关于x的函数关系式；
  （2）需要建多少座高压电线塔才能使y有最小值？最小值是多少？
  （参考数据：ln2≈0.69，ln10≈2.30）
  组卷：3引用：1难度：0.5

  解析

• 22．已知函数f（x）=[x²-（a+3）x+2a+3]e^x，a∈R，讨论函数f（x）的极值．
  组卷：15引用：1难度：0.6

  解析