2022-2023学年江苏省盐城市大丰区八年级（下）期中数学试卷
发布：2024/7/15 8:0:9
一、选择题（本大题共有8小题，每小题3分，共24分）
-
1．下列是五线谱中常用的符号，其中属于中心对称图形的是（ ）
组卷：18引用：1难度：0.9 -
2．以下调查中，最适合采用普查方式的是（ ）
组卷：36引用：2难度：0.9 -
3．下列事件是随机事件的是（ ）
组卷：174引用：4难度：0.7 -
4．掷一枚质地均匀的骰子，骰子停止后，在下列四个选项中，可能性最大的是（ ）
组卷：1183引用：5难度：0.5 -
5．吾悦广场开了一家特色美食店，开业一周后老板计划用统计图直观反映这周各天收入的起伏情况，下列各统计图中你认为最优的选择是（ ）
组卷：40引用：1难度：0.8 -
6．如图，把△ABC绕点C顺时针旋转40°得到△DEC，DE交AC于点G，若∠DGC=90°，则∠A的度数是（ ）组卷：120引用：2难度：0.7 -
7．用反证法证明“同旁内角不互补的两条直线不平行”时，应先提出的假设是（ ）
组卷：425引用：7难度：0.7 -
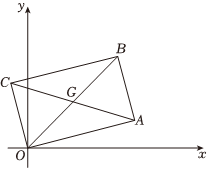8．如图，矩形OABC的顶点O为坐标原点，AC=4，对角线OB在第一象限的角平分线上．若矩形从图示位置开始绕点O以每秒45°的速度顺时针旋转，则当第2023秒时，矩形的对角线交点G的坐标为（ ）组卷：310引用：1难度：0.5
二、填空题（本大题共8小题，每小题3分，共24分）
-
9．每年的4月23日是“世界读书日”，某校为了解八年级350名学生对“世界读书日”的知晓情况，从中随机抽取了50名学生进行调查，则本次调查的样本容量是 ．
组卷：152引用：3难度：0.7
三、解答题（本大题共有11小题，共102分．解答时应写出文字说明、推理过程或演算步骤）
-
26．本学期我们研究了三角形的中位线的性质，回顾研究的过程，请回答以下问题：
（1）三角形中位线定理是：；
（2）梯形是有一组对边平行，另一组对边不平行的四边形，连接梯形两腰的中点，得到的线段叫做梯形的中位线．如图①，EF就是梯形ABCD的中位线，梯形的中位线具有什么性质呢？
小明思考之后给出了如下的证明思路：
如图②，连接AF并延长，交BC的延长线于点G．
先证△ADF和△GCF全等，再说明EF是△ABG的中位线．
…
经过你的分析，请写出梯形的中位线EF和两底AD、BC之间的关系：、；
（3）已知梯形的中位线长为7cm,高为6cm,则梯形面积是 cm2；
（4）如图③，直线l为▱ABCD外的任意一条直线，过A、B、C、D分别作直线l的垂线段BE、AF、CG、DH，请探索线段BE、AF、CG、DH之间的数量关系，并证明．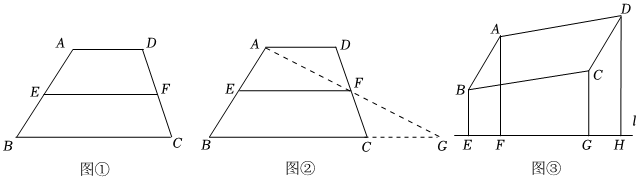
组卷：183引用：1难度：0.5 -
27．小亮在一次数学活动中，进行了如下的探究：
如图，在矩形ABCD中，AB=4，AD=3，以点B为中心将矩形ABCD旋转任意角度，得到矩形EBGF，点A、D、C的对应点分别为E、F、G．
（1）如图①，当点E落在CD边上时，求线段DE的长；
（2）如图②，当点E落在线段DF上时，BE与CD交于点H，求线段DH的长；
（3）如图③，若矩形ABCD的对角线AC、BD相交于点P，连接PF、PG，若△PFG面积为S，请直接写出S的取值范围 ．组卷：329引用：3难度：0.2
