2014年辽宁省沈阳市铁西区中考数学二模试卷
发布:2024/7/31 8:0:9
一、选择题(下列各题的四个选项中,只有一个是正确的,请将正确答案涂在答题卡上,每小题3分,共24分)
-
1.计算(-5)+(-7)的结果等于( )
组卷:769引用:4难度:0.8 -
 2.由一个圆柱与一个长方体组成的几何体如图所示,这个几何体的主视图是( )组卷:55引用:2难度:0.9
2.由一个圆柱与一个长方体组成的几何体如图所示,这个几何体的主视图是( )组卷:55引用:2难度:0.9 -
3.下列运算正确的是( )
组卷:9引用:1难度:0.9 -
4.已知线段AB,在线段AB上任取一点C,则线段BC≥2AC的概率是( )
组卷:2引用:1难度:0.7 -
 5.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )组卷:98引用:6难度:0.7
5.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )组卷:98引用:6难度:0.7 -
6.方程x(x-2)+x-2=0的解为( )
组卷:343引用:7难度:0.9 -
7.若不为0的两个实数a,b满足a+b=0,且a<b,则函数y=ax+b的图象可能是( )
组卷:108引用:2难度:0.7 -
 8.在平面直角坐标系中,直线y=kx(k为常数,且k≠0)与抛物线y=x2-2交于A,B两点,且点A的坐标为(-13,-1),点P的坐标为(0,-5),连接PA、PB.则下列结论正确的是( )3组卷:24引用:1难度:0.5
8.在平面直角坐标系中,直线y=kx(k为常数,且k≠0)与抛物线y=x2-2交于A,B两点,且点A的坐标为(-13,-1),点P的坐标为(0,-5),连接PA、PB.则下列结论正确的是( )3组卷:24引用:1难度:0.5
七、(本题12分)
-
24.已知,点M是△ABC的边BC的中点,分别以AB和AC为斜边,向△ABC的外侧画等腰直角三角形ABD和等腰直角三角形ACE,连接MD、ME.
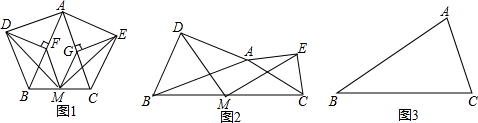
(1)如图1,在△ABC中,AB=AC,DF⊥AB于点F,EG⊥AC于点G,连接MF、MG,求证:MF=MG,MD=ME;
(2)如图2,△ABC是钝角三角形,且AB≠AC,其他条件不变,那么MD=ME还成立吗?说明理由;
(3)如图3,在任意△ABC中,仍分别以AB和AC为斜边,在∠BAC的内部画等腰直角三角形ABD和等腰直角三角形ACE,M是BC的中点,连接MD、ME和DE,请在图3中画出正确的图形,并直接写出△MED的形状.组卷:35引用:1难度:0.1
八、(本题14分)
-
25.如图,抛物线y=x2-2x+c与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为点D,点A的坐标为(-1,0).
(1)求抛物线的函数表达式;
(2)连接BC、CD、BD,判断△BCD的形状,并说明理由;
(3)连接AC,点M是抛物线y=x2-2x+c的对称轴上的一点,当△MAC是等腰三角形时,求点M的坐标;
(4)延长AC,BD交于点E,过点P(-4,0)作直线PQ与抛物线交于点N,与直线AC于点F,当∠PFA=∠E时,求点N的坐标.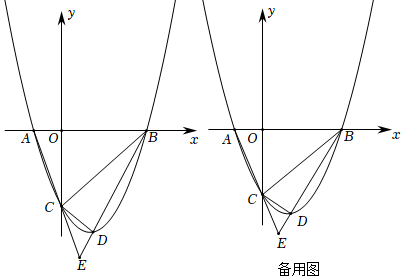 组卷:87引用:1难度:0.1
组卷:87引用:1难度:0.1


