2022-2023学年江苏省扬州市高三（上）期中数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合要求）

• 1．已知全集U={1，2，3，4，5}，集合M={1，2}，N={1，2，3，4}，则（∁_UM）∩N=（　　）

  A．{5}

  B．{3，4}

  C．{3，4，5}

  D．{1，2，3，4，5}
  组卷：2引用：2难度：0.7

  解析

• 2．

  1

  -

  tan

  15

  °

  1

  +

  tan

  15

  °

  的值为（　　）

  A．1

  B． 3 3

  C． 2 2

  D． 3
  组卷：344引用：7难度：0.9

  解析

• 3．古希腊数学家阿基米德的墓碑，上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等，相传这个图形表达了阿基米德最引以为自豪的发现，即：圆柱的内切球体积与圆柱体积比为定值，则该定值为（　　）

  A． 1 2

  B． 2 3

  C． 3 4

  D． 3 2
  组卷：12引用：2难度：0.7

  解析

• 4．

  （

  x

  -

  2

  ）

  （

  x

  -

  2

  x

  ）

  6

  的展开式中x的系数为（　　）

  A．-280

  B．-40

  C．40

  D．280
  组卷：35引用：3难度：0.5

  解析

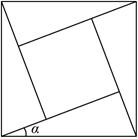• 5．我国古代数学家赵爽在注解《周髀算经》一书时介绍了“赵爽弦图”，它是由四个全等的直角三角形与一个小正方形拼成的大正方形如图所示，记直角三角形较小的锐角为α，大正方形的面积为S₁，小正方形的面积为S₂，若

  S

  1

  S

  2

  =

  5

  ，则sinα+cosα的值为（　　）

  A． 3 5 5

  B． 2 5 5

  C． 7 5

  D． 8 5
  组卷：1383引用：3难度：0.5

  解析

• 6．已知函数f（x）的导函数f′（x）满足f'（x）=f（x），则不等式

  f

  （

  x

  ）

  ＞

  2

  e

  π

  3

  cosx

  在区间

  （

  0

  ，

  π

  2

  ）

  上的解集为（　　）

  A． （ 0 ， π 6 ）

  B． （ π 6 ， π 3 ）

  C． （ π 3 ， π 2 ）

  D． （ 0 ， π 3 ）
  组卷：17引用：2难度：0.7

  解析

• 7．甲、乙、丙、丁四人各掷骰子5次（骰子出现的点数可能为1，2，3，4，5，6），并分别记录自己每次出现的点数，四人根据统计结果对自己的试验数据分别做了如下描述，可以判断一定出现6点的描述是（　　）

  A．中位数为4，众数为4

  B．中位数为3，极差为4

  C．平均数为3，方差为2

  D．平均数为4，第25百分位数为2
  组卷：37引用：4难度：0.6

  解析

四、解答题（本大题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤）

• 21．甲、乙两名学生进行“趣味投篮比赛”，制定比赛规则如下：每轮比赛中甲、乙两人各投一球，两人都投中或者都未投中则均记0分；一人投中而另一人未投中，则投中的记1分，未投中的记-1分，设每轮比赛中甲投中的概率为

  2

  3

  ，乙投中的概率为

  1

  2

  ，甲、乙两人投篮相互独立，且每轮比赛互不影响．
  （1）经过1轮比赛，记甲的得分为X，求X的分布列和期望；
  （2）经过3轮比赛，用P_n（n=1，2，3）表示第n轮比赛后甲累计得分低于乙累计得分的概率，研究发现点（n,P_n）（n=1，2，3）均在函数f（x）=m（s-t^x）的图象上，求实数m,s,t的值．
  组卷：25引用：4难度：0.6

  解析

• 22．已知函数f（x）=（x+2-ae^2x）e^x，其中e为自然对数的底数．
  （1）当a=0时，求函数f（x）的单调区间；
  （2）当a＞0时，
  （i）若f（x）≤1恒成立，求实数a的最小值；
  （ii）若f（x）存在最大值，求实数a的取值范围．
  组卷：13引用：2难度：0.3

  解析