2023-2024学年上海市嘉定一中高三（上）开学数学试卷

一、填空题（本大题共有12题，满分54分，第1-6题每题4分，第7-12题每题5分）考生应在答题纸的相应位置直接填写结果。

• 1．已知A={y|y=x²+1}，B={x|x＜3}，则A∪B=

  ．
  组卷：40引用：2难度：0.7

  解析

• 2．若x＞0，则x+

  2

  x

  的最小值为

   

  ．
  组卷：54引用：7难度：0.7

  解析

• 3．函数y=x²-6x+3，x∈[-1，4]的值域是

  ．
  组卷：926引用：2难度：0.8

  解析

• 4．已知

  sinα

  =

  4

  5

  ，则

  cos

  （

  α

  +

  π

  2

  ）

  =

  ．
  组卷：1518引用：9难度：0.9

  解析

• 5．已知直线l₁：x+y=0和l₂：2x-ay+3=0（a∈R），若l₁⊥l₂，则a=

  ．
  组卷：146引用：4难度：0.8

  解析

• 6．设向量

  a

  、

  b

  满足|

  a

  |=1，

  a

  •

  b

  =2，则

  a

  •（

  a

  +

  b

  ）=

  ．
  组卷：151引用：3难度：0.8

  解析

• 7．已知首项为2的等比数列{b_n}的公比为

  1

  3

  ，则这个数列所有项的和为

  ．
  组卷：162引用：3难度：0.7

  解析

三、解答题（本大题共有5题，满分39分）解答下列各题必须在答题纸的相应位与出必要的步骤.

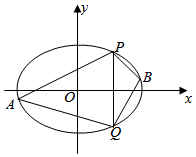• 20．已知椭圆C的中心在原点，焦点在x轴上，离心率为

  1

  2

  ，短轴长为4

  3

  ．
  （1）求椭圆C的标准方程；
  （2）直线x=2与椭圆C交于P，Q两点，A，B是椭圆C上位于直线PQ两侧的动点，且直线AB的斜率为

  1

  2

  ．
  （i）求四边形APBQ面积的最大值；
  （ii）设直线PA的斜率为k₁，直线PB的斜率为k₂，判断k₁+k₂的值是否为常数，并说明理由．
  组卷：1710引用：15难度：0.1

  解析

• 21．已知函数f（x）=ae^x-be^-x-（a+1）x（a、b∈R）．
  （1）当a=2，b=0时，求函数图像过点（0，f （0））的切线方程；
  （2）当b=1时，f（x）既存在极大值，又存在极小值，求实数a的取值范围；
  （3）当a∈（0，1），b=1时，x₁、x₂分别为f（x）的极大值点和极小值点，且f（x₁）+kf（x₂）＞0，求实数k的取值范围．
  组卷：200引用：7难度：0.3

  解析