2023-2024学年广东省江门市新会一中等高一(下)联考数学试卷(5月份)
发布:2025/11/8 12:0:21
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.已知G为△ABC的重心(三条中线的交点),
,∠BAC=2π3,则AB•AC=-2的最小值为( )|AG|组卷:204引用:5难度:0.6 -
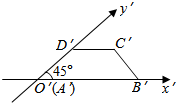 2.如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1,下底为的等腰梯形,那么原平面图形的面积为( )2+1组卷:348引用:3难度:0.8
2.如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1,下底为的等腰梯形,那么原平面图形的面积为( )2+1组卷:348引用:3难度:0.8 -
3.“欢乐颂”是尊称为“乐圣”“交响乐之王”的神圣罗马帝国音乐家贝多芬一生创作的重要作品之一.如图,如果以时间为横轴、音高为纵轴建立平面直角坐标系,那么写在五线谱中的音符就变成了坐标系中的点,如果这些点恰好在函数
的图象上,且图象过点y=4sin(ωx+φ)(ω>0,|φ|<π2),相邻最大值与最小值之间的水平距离为(π24,2),则是函数的单调递增区间的是( )π2 组卷:243引用:7难度:0.6
组卷:243引用:7难度:0.6 -
4.要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象( )
组卷:1006引用:64难度:0.9 -
5.已知平面向量
,a的夹角为b,且π3,|a|=2,则b=(-1,3)在a方向上的投影向量为( )b组卷:116引用:2难度:0.7 -
6.i2021的虚部为( )
组卷:115引用:3难度:0.9 -
7.在△ABC中,内角A,B,C所对的边分别是a,b,c,若c2=(a-b)2+6,C=
,则△ABC的面积是( )π3组卷:521引用:17难度:0.7 -
8.已知四棱锥S-ABCD的底面为矩形,SA⊥底面ABCD,点E在线段BC上,以AD为直径的圆过点E.若SA=
AB=3,则△SED的面积的最小值为( )3组卷:186引用:5难度:0.5
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分。
-
9.在△ABC所在平面内,点满足
,其中λ∈(0,+∞),m,n∈R,m≠0,n≠0,则下列说法正确的是( )AP=λ(ABm|AB|+ACn|AC|)组卷:142引用:9难度:0.5 -
10.下列结论正确的是( )
组卷:110引用:3难度:0.8 -
11.系统找不到该试题
三、填空题:本题共3小题,每小题5分,共15分。
-
12.函数f(x)=|asin2x+cos2x|+|sinx+cosx|•|(1+a)sinx+(1-a)cosx|,a∈R,且f(x)的最大值为3,则实数a=.
组卷:22引用:2难度:0.4 -
13.平行向量(共线向量):方向 的非零向量.
组卷:18引用:2难度:0.8 -
14.已知某圆台的上底面和下底面的面积分别为4π,9π,该圆台的体积为38π,则该圆台的高为 .
组卷:10引用:3难度:0.7
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15.已知△ABC的三个内角分别为A、B、C,其对边分别为a、b、c,若
.2c-ab+cosC=tanBsinC
(1)求角B的值;
(2)若b=2,求△ABC面积S的最大值.组卷:144引用:3难度:0.5 -
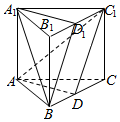 16.如图所示,三棱柱ABC-A1B1C1,D是BC的中点,D1是B1C1的中点.求证:
16.如图所示,三棱柱ABC-A1B1C1,D是BC的中点,D1是B1C1的中点.求证:
(1)A1B∥平面AC1D;
(2)平面A1BD1∥平面AC1D.组卷:498引用:2难度:0.5 -
17.已知
=(asinx,m+cosx),3=(cosx,-m+cosx),且f(x)=b.a•b
(1)求函数f(x)的解析式;
(2)当x∈[-,π6]时,f(x)的最小值是-4,求此时函数f(x)的最大值,并求出相应的x的值.π3组卷:25引用:2难度:0.5 -
18.在平面直角坐标系xOy中,角α终边与单位圆O的交点为E,将向量
逆时针方向旋转90°,得到向量OE,记A(1,0),B(0,-1).OF
(1)判断向量与AE的位置关系,并说明理由;BF
(2)求的最大值.|AE+AF|组卷:44引用:2难度:0.5 -
19.已知
=(asinx,m+cosx),3=(cosx,-m+cosx),且f(x)=b.a•b
(1)求函数f(x)的解析式;
(2)当x∈[-,π6]时,f(x)的最小值是-4,求此时函数f(x)的最大值,并求出相应的x的值.π3组卷:319引用:34难度:0.5


