当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市大足区八年级（上）期末数学试卷

发布：2024/7/11 8:0:9

一．选择题（本大题共12小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

1．下面四幅画分别是体育运动长鼓舞，武术，举重、摔跤抽象出来的简笔画，其中是轴对称图形的是（　　）
A． B． C． D．
组卷：367引用：13难度：0.9
解析
2．下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（　　）
A．3，4，9 B．5，5，12 C．8，7，15 D．13，12，22
组卷：91引用：3难度：0.7
解析
3．如果分式
2
x
x
-
1
有意义，那么x的取值范围是（　　）
A．x≠0 B．x≠1 C．x≠-1 D．x≠0且x≠1
组卷：101引用：2难度：0.8
解析
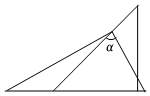4．如图，一副具有30°和45°角的直角三角板，按如图所示叠放在一起，则图中∠α的度数是（　　）
A．40° B．45° C．65° D．75°
组卷：264引用：4难度：0.7
解析
5．已知：点A（m-1，2）与点B（1，n+1）关于x轴对称，则m+n的值为（　　）
A．0 B．1 C．-1 D．2
组卷：183引用：2难度：0.8
解析
6．下列运算正确的是（　　）
A．（x³）²=x⁵ B．3x²+2x²=5x⁴
C．x⁸÷x²=x⁴ D．（2xy）²=4x²y²
组卷：143引用：2难度：0.8
解析
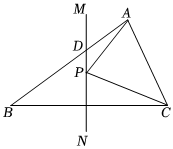7．如图，在△ABC中，AC=2，AB=3，BC=3.5，BC的垂直平分线MN交AB于点D，P是直线MN上的任意一点，则PA+PC的最小值是（　　）
A．2 B．3 C．3.5 D．4.5
组卷：1056引用：5难度：0.7
解析
8．用如图所示的几何图形的面积可以解释的代数恒等式是（　　）
A．（2a）²=4a² B．（a+b）²=a²+2ab+b²
C．2a（a+b）=2a²+2ab D．2a（2a+b）=4a²+2ab
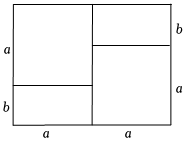组卷：1217引用：8难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：（本大题7个小题，每个小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答过程书写在对应的位置上．

24．已知一个各个数位上的数字均不为0的四位正整数
M
=
abcd
（
a
＞
c
）
，以它的百位数字作为十位，个位数字作为个位，组成一个新的两位数s,若s等于M的千位数字与十位数字的平方差，则称这个数M为“平方差数”，将它的百位数字和千位数字组成两位数
ba
，个位数字和十位数字组成两位数
dc
，并记
T
（
M
）
=
ba
+
dc
．
例如：6237是“平方差数”，因为6²-3²=27，所以6237是“平方差数”；
此时T（6237）=26+73=99．
又如：5135不是“平方差数”，因为5²-3²=16≠15，所以5135不是“平方差数”．
（1）判断7425是否是“平方差数”？并说明理由；
（2）若
M
=
abcd
是“平方差数”，且T（M）比M的个位数字的9倍大30，求所有满足条件的“平方差数”M．
组卷：416引用：5难度：0.5
解析
25．在等边△ABC中，D为BC上一点，E为BA上一点，过B作BF∥AC，连接EF，DF，且∠EFD=60°．

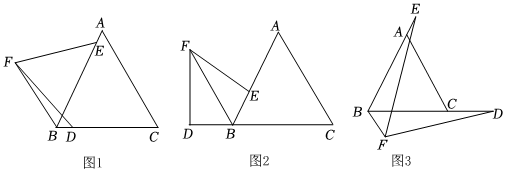
（1）如图1，若BF=4，BE=5，求BD的长．
（2）如图2，若D为CB延长线上一点，试探究BD、BE、BF的关系，并说明理由．
（3）如图3，若D为BC延长线上一点，E为BA延长线上一点，AE：BF：AC=2：3：5，请直接写出CD：BD的比值．
组卷：176引用：2难度：0.1
解析