当前位置：试卷中心 > 试卷详情

2023-2024学年安徽省六校教育研究会高一（上）入学数学试卷

发布：2025/11/7 3:0:41

一、单选题（共10小题，每小题3分，共30分）

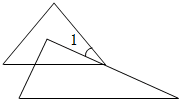1．将一副三角板如图所示放置，斜边平行，则∠1的度数为（　　）
A．5° B．10° C．15° D．20°
组卷：26引用：2难度：0.9
2．如图，分别延长圆内接四边形ABCD两组对边相交于E和F两点，如果∠E=30°，∠F=50°，那么∠A为（　　）
A．55° B．50° C．45° D．40°
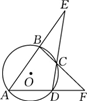组卷：10引用：1难度：0.9
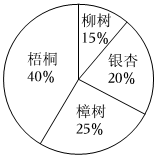3．为了树立和践行绿水青山就是金山银山的理念，A市某高中全体教师于2023年3月12日开展植树活动，购买柳树、银杏、梧桐、樟树四种树苗共计600棵，比例如图所示．青年教师、中年教师、老年教师报名参加植树活动的人数之比为5：3：2，若每种树苗均按各年龄段报名人数的比例进行分配，则中年教师应分得梧桐的数量为（　　）
A．30棵 B．50棵 C．72棵 D．80棵
组卷：92引用：3难度：0.7
4．若方程a-2lnx=-x²-1在
x
∈
[
1
e
2
，
e
2
]
上有解，则实数a的取值范围是（　　）
A．
[
1
-
e
2
，-
3
-
1
e
2
]
B．[3-e⁴，-2]
C．
[
-
5
-
1
e
4
，
+
∞
）
D．[1-e²，-2]
组卷：110引用：3难度：0.4
5．找规律填数字是一项很有趣的游戏，特别锻炼观察和思考能力，按照“1=7”“2=14”“3=42”“4=168”的规律，可知5=（　　）
A．490 B．62 C．720 D．840
组卷：18引用：1难度：0.7
6．在锐角△ABC中，角A，B，C所对的边分别为a,b,c.若2ccosB=a-c,则
sin
（
A
-
C
）
sin
B
的取值范围为（　　）
A．
（
1
，
3
）
B．（0，1） C．
（
0
，
2
）
D．
（
2
，
3
）
组卷：475引用：6难度：0.6
7．不等式ax²-x-c＞0的解集为{x|-2＜x＜1}，则函数y=ax²+x-c的图象为（　　）
A． B．
C． D．
组卷：128引用：4难度：0.8
8．2013年9月7日，习近平总书记在哈萨克斯坦纳扎尔巴耶夫大学发表演讲并回答学生们提出的问题，在谈到环境保护问题时他指出：“我们既要绿水青山，也要金山银山．宁要绿水青山，不要金山银山，而且绿水青山就是金山银山．”“绿水青山就是金山银山”这一科学论断，成为树立生态文明观、引领中国走向绿色发展之路的理论之基．某市为了改善当地生态环境，2014年初投入资金160万元，以后每年投入资金比上一年增加30万元，从2020年初开始改变投资方案，每年投入资金比上一年增加10%，则从2014年初到2024年底该市生态环境建设投资总额大约为（参考数据：1.1⁵≈1.610，1.1⁶≈1.771）（　　）
A．3800万元 B．3490万元 C．3301万元 D．2991万元
组卷：5引用：2难度：0.7
9．关于x的一元二次方程x²+（a²-1）x+a-2=0有一个根小于-1，另一个根大于1，则a的取值范围是（　　）
A．（-2，1） B．（-2，0） C．（0，1） D．（1，2）
组卷：142引用：4难度：0.7
10．日本政府不顾国内外的质疑和反对，单方面决定以排海的方式处置福岛核电站事故的核污水，这种极不负责任的做法将严重损害国际公共健康安全和周边国家人民的切身利益．福岛核污水中含有多种放射性物质，其中放射性物质³H含量非常高，它可以进入生物体内，还可以在体内停留，并引起基因突变，但却难以被清除．现已知³H的质量M（kg）随时间t（年）的指数衰减规律是：M=M₀•a^-0.008t（其中M₀为³H的初始质量）．已知经过125年³H的质量衰减为最初的
1
2
，则当³H的质量衰减为最初的
1
8
时，所经过的时间为（　　）
A．325年 B．375年 C．600年 D．1000年
组卷：60引用：1难度：0.9

二、填空题（共4小题，每小题3分，共12分）

11．总体是由编号为01，02，⋯，29，30的30个个体组成．利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为
．
7816
1572
0802
6315
0216
4319
9714
0198
3204
9234
4936
8200
3623
4869
6938
7181
组卷：442引用：6难度：0.7
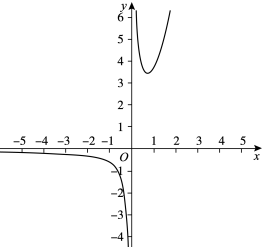12．已知下列五个函数：y=x,y=
1
x
，y=x²，y=lnx,y=e^x，从中选出两个函数分别记为f（x）和g（x），若F（x）=f（x）+g（x）的图象如图所示，则F（x）=
．
组卷：160引用：5难度：0.7
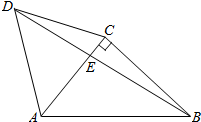13．如图，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB=90°，BD交AC于E，AB=2，则AE=
．
组卷：90引用：6难度：0.5
14．已知数列{a_n}中，a₁≠0，
a
m
+
n
=
a
m
a
n
（
m
,
n
∈
N
*
）
，且a₃、a₁₁是函数f（x）=2x²+19x+20的两个零点，则a₇=
．
组卷：44引用：2难度：0.5

三、解答题（共8小题，共58分）

15．把下列各式因式分解：
（1）a³-a+2b-2a²b；
（2）（x²+3x）²-2（x²+3x）-8．
组卷：40引用：1难度：0.7
16．已知a∈R，当x＞0时，f（x）=log₂（
1
x
+a）．
（Ⅰ）若函数f（x）过点（1，1），求此时函数f（x）的解析式；
（Ⅱ）若函数g（x）=f（x）+2log₂x只有一个零点，求实数a的值．
组卷：91引用：4难度：0.5
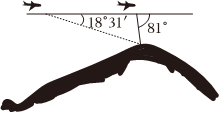17．如图，飞机的航线和山顶在同一个铅直平面内，已知飞机的高度为海拔20250m,速度为189km/h,飞行员先看到山顶的俯角为18°30′，经过960s后，又看到山顶的俯角为81°，求山顶的海拔高度．（精确到1m）
组卷：14引用：2难度：0.5
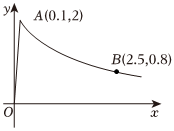18．为了预防流感，某学校对教室进行药熏消毒．室内每立方米空气的含药量y（单位：毫克）随时间x（单位：h）的变化情况如图所示，在药物释放过程中，y与x成正比（对应图中OA）；药物释放完毕后，y与x函数关系式为y=k•（x+a）^-1（k为常数，其图象经过点B）．根据图中提供的信息，回答下列问题：
（1）写出从药物释放开始，y与x之间的函数关系式；
（2）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室．学校每天19：00准时对教室进行药熏消毒，那么第二天6：30后，学生能否进教室？并说明理由．
组卷：43引用：2难度：0.5
19．我们定义：如果三角形上两点，其中一点为一边的中点，如果这两点的连线将三角形分成周长相等的两部分，我们称这条线段为该三角形的“等分周线”．如图1，在△ABC中，D是BC的中点，点E在AB上，若BD+BE=CD+AC+AE，则DE为△ABC的一条“等分周线”．

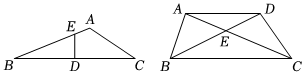
（1）任意三角形的“等分周线”有_____条，若某三角形的“等分周线”的一个端点是三角形的顶点，则这个三角形是_____．
（2）如图1，在△ABC中，D是BC的中点，点E在AB上，DE为△ABC的一条“等分周线”．若AB＞AC，设∠A=n°，AC=m,求DE的长（用含m,n的代数式表示）．
（3）如图2，在四边形ABCD中，BC=2CD，AC平分∠BCD，BA⊥AC，点E在AC上，连接ED，EB，
AB
=
3
，
EC
=
3
+
1
，∠BEC=120°，求ED的长．
组卷：10引用：2难度：0.5
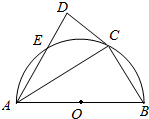20．已知AB为半圆O的直径，AB=4，C为半圆上一点，过点C作半圆的切线CD，过点A作AD⊥CD于D，交半圆于点E，DE=1．
（Ⅰ）求证：AC平分∠BAD；
（Ⅱ）求BC的长．
组卷：184引用：54难度：0.5

21．高三（1）班学生每周用于数学学习时间x（单位：h）与数学成绩y（单位：分）之间有如下数据：

x 24 15 23 19 16 11 20 16 17 13

y 92 79 97 89 64 47 83 68 71 59

根据上述提供的数据，你会提出哪些问题？针对自己提出的问题，请设计你解决问题的思路，及主要的解决过程，在此基础上，提出你独特的看法．

组卷：29引用：1难度：0.5

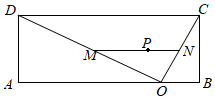22．某学校在平面图为矩形的操场ABCD内进行体操表演，其中AB=40，BC=15，O为AB上一点，且BO=10，线段OC、OD、MN为表演队列所在位置（M、N分别在线段OD、OC上），△OCD内的点P为领队位置，且P到OC、OD的距离分别为
13
、
5
，记OM=d,我们知道当△OMN面积最小时观赏效果最好．
（1）当d为何值时，P为队列MN的中点；
（2）怎样安排M的位置才能使观赏效果最好？求出此时△OMN的面积．
组卷：180引用：3难度：0.7

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． [ 1 - e 2 ，- 3 - 1 e 2 ]	B．[3-e⁴，-2]
C． [ - 5 - 1 e 4 ， + ∞ ）	D．[1-e²，-2]

7816	1572	0802	6315	0216	4319	9714	0198
3204	9234	4936	8200	3623	4869	6938	7181

A．	B．
C．	D．

2023-2024学年安徽省六校教育研究会高一（上）入学数学试卷

一、单选题（共10小题，每小题3分，共30分）

1．将一副三角板如图所示放置，斜边平行，则∠1的度数为（ ）

2．如图，分别延长圆内接四边形ABCD两组对边相交于E和F两点，如果∠E=30°，∠F=50°，那么∠A为（ ）

4．若方程a-2lnx=-x2-1在x∈[1e2，e2]上有解，则实数a的取值范围是（ ）

5．找规律填数字是一项很有趣的游戏，特别锻炼观察和思考能力，按照“1=7”“2=14”“3=42”“4=168”的规律，可知5=（ ）

6．在锐角△ABC中，角A，B，C所对的边分别为a,b,c.若2ccosB=a-c,则sin（A-C）sinB的取值范围为（ ）

7．不等式ax2-x-c＞0的解集为{x|-2＜x＜1}，则函数y=ax2+x-c的图象为（ ）

9．关于x的一元二次方程x2+（a2-1）x+a-2=0有一个根小于-1，另一个根大于1，则a的取值范围是（ ）

二、填空题（共4小题，每小题3分，共12分）

12．已知下列五个函数：y=x,y=1x，y=x2，y=lnx,y=ex，从中选出两个函数分别记为f（x）和g（x），若F（x）=f（x）+g（x）的图象如图所示，则F（x）=．

13．如图，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB=90°，BD交AC于E，AB=2，则AE=．

14．已知数列{an}中，a1≠0，am+n=aman（m,n∈N*），且a3、a11是函数f（x）=2x2+19x+20的两个零点，则a7=．

三、解答题（共8小题，共58分）

15．把下列各式因式分解：（1）a3-a+2b-2a2b；（2）（x2+3x）2-2（x2+3x）-8．

16．已知a∈R，当x＞0时，f（x）=log2（1x+a）．（Ⅰ）若函数f（x）过点（1，1），求此时函数f（x）的解析式；（Ⅱ）若函数g（x）=f（x）+2log2x只有一个零点，求实数a的值．

17．如图，飞机的航线和山顶在同一个铅直平面内，已知飞机的高度为海拔20250m,速度为189km/h,飞行员先看到山顶的俯角为18°30′，经过960s后，又看到山顶的俯角为81°，求山顶的海拔高度．（精确到1m）

20．已知AB为半圆O的直径，AB=4，C为半圆上一点，过点C作半圆的切线CD，过点A作AD⊥CD于D，交半圆于点E，DE=1．（Ⅰ）求证：AC平分∠BAD；（Ⅱ）求BC的长．

1．将一副三角板如图所示放置，斜边平行，则∠1的度数为（　　）

2．如图，分别延长圆内接四边形ABCD两组对边相交于E和F两点，如果∠E=30°，∠F=50°，那么∠A为（　　）

4．若方程a-2lnx=-x²-1在
x
∈
[
1
e
2
，
e
2
]
上有解，则实数a的取值范围是（　　）

5．找规律填数字是一项很有趣的游戏，特别锻炼观察和思考能力，按照“1=7”“2=14”“3=42”“4=168”的规律，可知5=（　　）

6．在锐角△ABC中，角A，B，C所对的边分别为a,b,c.若2ccosB=a-c,则
sin
（
A
-
C
）
sin
B
的取值范围为（　　）

7．不等式ax²-x-c＞0的解集为{x|-2＜x＜1}，则函数y=ax²+x-c的图象为（　　）

9．关于x的一元二次方程x²+（a²-1）x+a-2=0有一个根小于-1，另一个根大于1，则a的取值范围是（　　）

12．已知下列五个函数：y=x,y=
1
x
，y=x²，y=lnx,y=e^x，从中选出两个函数分别记为f（x）和g（x），若F（x）=f（x）+g（x）的图象如图所示，则F（x）=
．

13．如图，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB=90°，BD交AC于E，AB=2，则AE=
．

14．已知数列{a_n}中，a₁≠0，
a
m
+
n
=
a
m
a
n
（
m
,
n
∈
N
*
）
，且a₃、a₁₁是函数f（x）=2x²+19x+20的两个零点，则a₇=
．

15．把下列各式因式分解：
（1）a³-a+2b-2a²b；
（2）（x²+3x）²-2（x²+3x）-8．

16．已知a∈R，当x＞0时，f（x）=log₂（
1
x
+a）．
（Ⅰ）若函数f（x）过点（1，1），求此时函数f（x）的解析式；
（Ⅱ）若函数g（x）=f（x）+2log₂x只有一个零点，求实数a的值．

20．已知AB为半圆O的直径，AB=4，C为半圆上一点，过点C作半圆的切线CD，过点A作AD⊥CD于D，交半圆于点E，DE=1．
（Ⅰ）求证：AC平分∠BAD；
（Ⅱ）求BC的长．