2021-2022学年云南省部分学校高二(上)联考数学试卷(10月份)
发布:2025/11/6 18:0:40
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=4,E是BC的中点,F满足
,则异面直线AE,CF所成角的余弦值为( )AF=14AD组卷:205引用:3难度:0.6 -
2.已知点G为三角形ABC的重心,且
,当∠C取最大值时,cosC=( )|GA+GB|=|GA-GB|组卷:497引用:9难度:0.4 -
3.已知复数z满足z•i=2+i,则z=( )
组卷:28引用:3难度:0.8 -
4.已知向量
,平面α的一个法向量AB=(2,4,x),若AB∥α,则( )n=(1,y,3)组卷:112引用:3难度:0.8 -
5.记△ABC的内角A,B,C的对边分别为a,b,c,且2sin2A+2sin2B=2sin2(A+B)+3sinAsinB,则cosC=( )
组卷:240引用:4难度:0.5 -
6.若直线a的方向向量为
,平面α,β的法向量分别为a,n,则下列命题为假命题的是( )m组卷:139引用:3难度:0.7 -
7.已知集合A={0,1},B={1,2,3},则A∩B=( )
组卷:92引用:3难度:0.7 -
8.在三棱锥A-BCD中,AB=AC=AD=6,AB,AC,AD两两垂直,E为AB的中点,F为AD上更靠近点D的三等分点,O为△BCD的重心,则O到直线EF的距离为( )
组卷:155引用:5难度:0.6 -
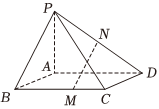 9.四棱锥P-ABCD底面ABCD为平行四边形,M,N分别为棱BC,PD上的点,,PN=ND,设CMCB=13,AB=a,AD=b,则向量AP=c用基底MN表示为( ){a,b,c}
9.四棱锥P-ABCD底面ABCD为平行四边形,M,N分别为棱BC,PD上的点,,PN=ND,设CMCB=13,AB=a,AD=b,则向量AP=c用基底MN表示为( ){a,b,c}
组卷:456引用:6难度:0.7 -
10.已知函数
,若方程y=f(x)-m有4个不同的零点x1,x2,x3,x4,且x1<x2<x3<x4,则f(x)=|log2(x-1)|,1<x≤3x2-10x+22,x>3=( )(1x1+1x2)(x3+x4)组卷:225引用:3难度:0.5 -
11.下表是某校在2022年高考中各班的最高分,则这组数据从小到大的第80百分位数是( )
班级 最高分 班级 最高分 1班 694 7班 658 2班 701 8班 677 3班 689 9班 642 4班 691 10班 656 5班 681 11班 673 6班 666 12班 638 组卷:78引用:2难度:0.9 -
 12.已知一组数据的频率分布直方图如图所示,则数据的中位数估计值为( )组卷:414引用:6难度:0.9
12.已知一组数据的频率分布直方图如图所示,则数据的中位数估计值为( )组卷:414引用:6难度:0.9
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
-
13.已知直线l的一个方向向量为
,平面α的一个法向量为d=(2,-1,3),且直线l与平面α平行,则实数t=.n=(1,t,0)组卷:61引用:2难度:0.7 -
14.已知集合
,任取k∈A,则幂函数y=xk为偶函数的概率为 .(结果用数值表示)A={-2,-1,-12,0,13,12,1,2,3}组卷:47引用:1难度:0.7 -
15.在平行六面体ABCD-A1B1C1D1中,已知∠BAD=∠A1AB=∠A1AD=60°,AD=4,AB=3,AA1=5,
=.|AC1|组卷:303引用:4难度:0.7 -
16.在三棱锥S-ABC中,SA=SB=CA=CB=AB=2,二面角S-AB-C的大小为60°,则三棱锥S-ABC的外接球的表面积为 .
组卷:54引用:3难度:0.5
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17.已知甲运动员的投篮命中率为0.8,乙运动员投篮命中率为0.7,甲、乙各投篮一次.设事件A为“甲投中”,事件B为“乙投中”.
(1)求甲、乙二人中恰有一人投中的概率;
(2)求甲、乙二人中至少有一人投中的概率.组卷:150引用:2难度:0.7 -
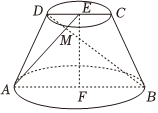 18.如图所示,四边形ABCD是圆台EF的轴截面,M是上底面圆周上异于C,D的一点,圆台的高,AB=2CD=4.EF=3
18.如图所示,四边形ABCD是圆台EF的轴截面,M是上底面圆周上异于C,D的一点,圆台的高,AB=2CD=4.EF=3
(1)证明:△AMB是直角三角形;
(2)是否存在点M使得平面ADM与平面DME的夹角的余弦值为?若存在,求出点M的位置;若不存在,请说明理由.55
组卷:67引用:4难度:0.4 -
19.△ABC中,三个内角A、B、C所对的边分别为a、b、c,若B=60°,a=(
-1)c.3
(1)求角A的大小;
(2)已知当x∈[,π6]时,函数f(x)=cos2x+asinx的最大值为3,求△ABC的面积.π2组卷:56引用:11难度:0.5 -
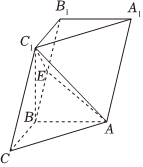 20.如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,,AB=CC1=2,BC=2,点E在棱BB1上.∠BCC1=π4
20.如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,,AB=CC1=2,BC=2,点E在棱BB1上.∠BCC1=π4
(1)证明:C1B⊥平面ABC;
(2)若BE=λBB1,试确定λ的值,使得C到平面AC1E的距离为.455组卷:48引用:4难度:0.6 -
21.已知k为实数,
.f(x)=2sin2(π4+x)-k•cos2x
(1)若k=0,求关于x的方程f(x)=1在[0,π]上的解;
(2)若,求函数y=f(x),x∈R的单调减区间;k=3
(3)已知a为实数且,若关于x的不等式|f(x)-a|<2在k=3时恒成立,求a的取值范围.x∈[π4,π2]组卷:79引用:4难度:0.5 -
22.已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x2+2x-3.
(1)求f(x)的解析式;
(2)若f(m+1)<f(2m-1),求实数m的取值范围.组卷:322引用:10难度:0.6


