2022-2023学年宁夏石嘴山市平罗中学高一（下）期末数学试卷

一、单选题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项符合题目要求。）

• 1．已知向量

  a

  =（t,1），

  b

  =（1，2）．若

  a

  ⊥

  b

  ，则实数t的值为（　　）

  A．-2

  B．2

  C． - 1 2

  D． 1 2
  组卷：410引用：10难度：0.7

  解析

• 2．新华中学高三年级有学生1100人，高二年级有学生900人，高一年级有学生1000人，现以年级为标准，用分层抽样的方法从这三个年级中抽取一个容量为150的样本进行某项研究，则应从高三年级学生中抽取的学生人数为（　　）

  A．45

  B．50

  C．55

  D．60
  组卷：67引用：3难度：0.7

  解析

• 3．某人射击一次，设事件A：“中靶”；事件B：“击中环数大于5”；事件C：“击中环数大于1且小于6”；事件D：“击中环数大于0且小于6”，则正确的关系是（　　）

  A．B与C为互斥事件	B．B与C为对立事件
  C．A与D为互斥事件	D．A与D为对立事件
  组卷：157引用：4难度：0.9

  解析

• 4．已知某圆锥的母线长为4，底面圆的半径为2，则圆锥的全面积为（　　）

  A．10π

  B．12π

  C．14π

  D．16π
  组卷：58引用：3难度：0.6

  解析

• 5．设m,n是不同的直线，α，β是不同的平面，则下列命题正确的是（　　）

  A．若m⊥n,n∥α，则m⊥α	B．若m∥β，β⊥α，则m⊥α
  C．若m⊥α，α⊥β，则m∥β	D．若m⊥α，m⊥β，则α∥β
  组卷：263引用：14难度：0.7

  解析

• 6．从分别写有1，2，3，4的4张卡片中随机抽取2张，则抽到的2张卡片上的数字之和是2的倍数的概率为（　　）

  A． 1 5

  B． 1 3

  C． 2 5

  D． 2 3
  组卷：113引用：2难度：0.7

  解析

• 7．在△ABC中，角A，B，C的对边分别为a,b,c,且

  si

  n

  2

  A

  2

  =

  c

  -

  b

  2

  c

  ，则△ABC是（　　）

  A．直角三角形	B．锐角三角形
  C．等边三角形	D．A=30°的三角形
  组卷：73引用：8难度：0.6

  解析

四、解答题（本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。）

• 21．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，AB⊥BC，PA=AD=4，BC=1，

  AB

  =

  3

  ，

  CD

  =

  2

  3

  ．
  （1）证明：DC⊥平面PAC；
  （2）求AD与平面PCD所成角的余弦值．
  组卷：317引用：7难度：0.5

  解析

• 22．甲、乙、丙、丁4名棋手进行象棋比赛，赛程如下面的框图所示，其中编号为i的方框表示第i场比赛，方框中是进行该场比赛的两名棋手，第i场比赛的胜者称为“胜者i“，负者称为“负者i“，第6场为决赛，获胜的人是冠军．已知甲每场比赛获胜的概率均为

  3

  4

  ，而乙、丙、丁相互之间胜负的可能性相同．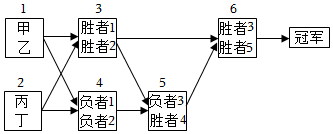
  
  （Ⅰ）求甲获得冠军的概率；
  （Ⅱ）求乙进入决赛，且乙与其决赛对手是第二次相遇的概率．
  组卷：201引用：3难度：0.7

  解析