当前位置：试卷中心 > 试卷详情

2021-2022学年山东省青岛市四区市高一（上）期中数学试卷

发布：2025/11/6 12:2:0

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设a=log₅4，则
b
=
log
1
5
1
3
，c=0.5^-0.2，则a,b,c的大小关系是（　　）
A．a＜b＜c B．b＜a＜c C．c＜b＜a D．c＜a＜b
组卷：2371引用：14难度：0.7
2．古希腊科学家阿基米德在《论平面图形的平衡》一书中提出了杠杆原理，它是使用天平称物品的理论基础，当天平平衡时，左臂长与左盘物品质量的乘积等于右臀长与右盘物品质量的乘积，某金店用一杆不准确的天平（两边臂不等长）称黄金，某顾客要购买10g黄金，售货员先将5g的砝码放在左盘，将黄金放于右盘使之平衡后给顾客；然后又将5g的砝码放入右盘，将另一黄金放于左盘使之平衡后又给顾客，则顾客实际所得黄金（　　）
A．大于10g B．小于10g
C．大于等于10g D．小于等于10g
组卷：127引用：6难度：0.6
3．已知集合M={x||x|＜3}，N={x|y=
6
+
x
-
x
2
}，则M∩N=（　　）
A．{x|-2＜x＜3} B．{x|-2≤x＜3} C．{x|-2＜x≤3} D．{x|-3＜x≤3}
组卷：78引用：4难度：0.8
4．函数
f
（
x
）
=
2
x
2
-
2
x
，x∈[0，3]的值域是（　　）
A．
[
1
2
，
8
]
B．（-∞，8] C．
[
1
2
，
+
∞
）
D．（0，8]
组卷：909引用：1难度：0.8
5．已知函数y=f（x）在定义域（-1，1）上是减函数，且f（2a-1）＜f（1-a），则实数a的取值范围是（　　）
A．（
2
3
，
+
∞
） B．（
2
3
，
1
）
C．（0，2） D．（0，+∞）
组卷：3563引用：24难度：0.9
6．函数
y
=
x
-
1
+
lg
（
3
-
x
）
的定义域为（　　）
A．（1，3） B．[1，3） C．（3，+∞） D．[1，+∞）
组卷：404引用：4难度：0.8
7．已知偶函数f（x）的定义域为R，当x∈[0，+∞）时，f（x）单调递增，则f（-2），f（π），f（-3）的大小关系是（　　）
A．f（π）＞f（-2）＞f（-3） B．f（π）＞f（-3）＞f（-2）
C．f（π）＜f（-2）＜f（-3） D．f（π）＜f（-3）＜f（-2）
组卷：108引用：12难度：0.6
8．下列函数中，在（0，+∞）上单调递增且值域为（0，+∞）的是（　　）
A．y=2^x B．
y
=
-
1
x
C．
y
=
x
D．y=lgx
组卷：99引用：1难度：0.7

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．下列函数中是偶函数，且在区间（0，+∞）上是减函数的是（　　）
A．y=|x|+1 B．y=x^-2 C．
y
=
1
x
-
x
D．y=2^-|x|
组卷：40引用：1难度：0.7
10．已知函数f（x）的导函数f'（x）的图象如图所示，则下列结论正确的是（　　）
A．f（x）有且仅有两个极值点
B．f（x）在区间（2，+∞）上单调递增
C．f（x）可能有四个零点
D．若f（x）在区间（m,n）上单调递减，则n-m的最大值为6
组卷：18引用：2难度：0.5
11．已知幂函数f（x）=（m²-2m-2）x^m的图象过点
（
2
，
1
2
）
，则（　　）
A．f（x）=x³
B．f（x）=x^-1
C．函数f（x）在（-∞，0）上为减函数
D．函数f（x）在（0，+∞）上为增函数
组卷：208引用：6难度：0.7

12．下列说法正确的是（　　）

A．若奇函数f（x）=x³+（b-1）x²+sinx的定义域为[a-1，2a+1]，则a+b=1

B．幂函数图像一定不过第四象限

C．

sin

（

）

最小正周期为π

D．若lna＜1，则a的取值范围是（-∞，e）

组卷：3引用：1难度：0.6

三、填空题：本题共4个小题，每小题5分，共20分．

13．甲乙丙三个学生同时参加了若干门学科竞赛至少包含数学和物理．在每科竞赛中，甲乙丙三人中都有一个学生的分数为x,另一个学生的分数为y,第三个学生的分数为z,其中x,y,z是三个互不相等的正整数．在完成所有学科竞赛后，甲的总分为47分，乙的总分为24分，丙的总分为16分．
（1）甲乙丙三个学生参加的学科竞赛门数为
（用x,y,z表示）；
（2）若在甲乙丙这三个学生中乙的数学竞赛成绩排名第一，则下列正确的序号为
．
①甲乙丙三个学生至少参加了四门学科竞赛；
②x,y,z这三个数中的最大值可以取到21；
③在甲乙丙这三个学生中，甲学生的物理竞赛成绩可能排名第二；
④在甲乙丙这三个学生中，丙学生的物理竞赛成绩一定排名第二．
组卷：18引用：1难度：0.3
14．已知x＞0，y＞0，2xy=x+y+4，则x+y的最小值为
．
组卷：376引用：12难度：0.6
15．已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=log₂（2-x），则f（0）+f（2）=
．
组卷：195引用：10难度：0.7
16．用有理数指数幂的形式表示
a
a
=
．
组卷：163引用：2难度：0.8

四、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

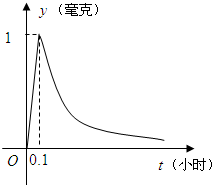17．为了预防流感，某学校对教室用药熏消毒法进行消毒．如图所示，已知药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，室内每立方米空气中的含药量y（毫克）与时间t（小时）的函数关系式为
y
=
（
1
16
）
t
-
a
（a为常数）．
（1）求常数a的值；
（2）求从药物释放开始，室内每立方米空气中的含药量y（毫克）与时间t（小时）之间的函数关系式；
（3）当药物释放完毕后，规定空气中每立方米的含药量不大于0.25毫克时，学生方可进入教室．问从药物释放开始，至少需要经过多少小时，学生才能回到教室？
组卷：24引用：1难度：0.3
18．已知定义在（-∞，0）∪（0，+∞）上的函数f（x）满足f（xy）+1=f（x）+f（y），且f（x）在（0，+∞）上单调递减．
（1）证明：函数f（x）是偶函数；
（2）解关于x的不等式f（x-1）+f（2）≥2．
组卷：124引用：2难度：0.5
19．已知函数f（x）是二次函数，且满足f（0）=1，f（x+1）-f（x）=2x+5；函数g（x）=a^x（a＞0且a≠1）
（1）求f（x）的解析式；
（2）若g（2）=
1
4
，且g[f（x）]≥k对x∈[-1，1]恒成立，求实数k的取值范围．
组卷：278引用：4难度：0.3
20．已知函数f（x）=log_a（x-2a）+log_a（x-3a）（a＞0且a≠1）．
（1）当
a
=
1
2
，求f（2）的值；
（2）当
a
=
1
2
时，若方程
f
（
x
）
=
lo
g
1
2
（
p
-
x
）
在（3，4）上有解，求实数p的取值范围；
（3）若f（x）≤1在[a+3，a+4]上恒成立，求实数a的取值范围．
组卷：177引用：3难度：0.4
21．已知集合A={x|x²-4x-5≥0}，集合B={x|2a≤x≤a+2}．
（1）若a=-1，求A∩B，A∪B；
（2）若A∩B=B，求实数a的取值范围．
组卷：653引用：5难度：0.5
22．设函数f（x）=ax²+bx+1（a,b为实数），
（1）若f（-1）=0且对任意实数x均有f（x）≥0成立，求f（x）表达式；
（2）在（1）的条件下，若g（x）=f（x）-kx,在区间[-2，2]上是单调函数，则实数k的取值范围；
（3）在（1）的条件下，
F
（
x
）
=
f
（
x
）

（
x
＞
0
）
-
f
（
x
）

（
x
＜
0
）
，当x∈[-2，2]且x≠0时，求F（x）的值域．
组卷：71引用：1难度：0.3

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．大于10g	B．小于10g
C．大于等于10g	D．小于等于10g

A．f（π）＞f（-2）＞f（-3）	B．f（π）＞f（-3）＞f（-2）
C．f（π）＜f（-2）＜f（-3）	D．f（π）＜f（-3）＜f（-2）

2021-2022学年山东省青岛市四区市高一（上）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设a=log54，则b=log1513，c=0.5-0.2，则a,b,c的大小关系是（ ）

3．已知集合M={x||x|＜3}，N={x|y=6+x-x2}，则M∩N=（ ）

4．函数f（x）=2x2-2x，x∈[0，3]的值域是（ ）

5．已知函数y=f（x）在定义域（-1，1）上是减函数，且f（2a-1）＜f（1-a），则实数a的取值范围是（ ）

6．函数y=x-1+lg（3-x）的定义域为（ ）

7．已知偶函数f（x）的定义域为R，当x∈[0，+∞）时，f（x）单调递增，则f（-2），f（π），f（-3）的大小关系是（ ）

8．下列函数中，在（0，+∞）上单调递增且值域为（0，+∞）的是（ ）

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．下列函数中是偶函数，且在区间（0，+∞）上是减函数的是（ ）

10．已知函数f（x）的导函数f'（x）的图象如图所示，则下列结论正确的是（ ）

11．已知幂函数f（x）=（m2-2m-2）xm的图象过点（2，12），则（ ）

12．下列说法正确的是（ ）

三、填空题：本题共4个小题，每小题5分，共20分．

14．已知x＞0，y＞0，2xy=x+y+4，则x+y的最小值为 ．

15．已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=log2（2-x），则f（0）+f（2）=．

16．用有理数指数幂的形式表示aa=．

四、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

18．已知定义在（-∞，0）∪（0，+∞）上的函数f（x）满足f（xy）+1=f（x）+f（y），且f（x）在（0，+∞）上单调递减．（1）证明：函数f（x）是偶函数；（2）解关于x的不等式f（x-1）+f（2）≥2．

19．已知函数f（x）是二次函数，且满足f（0）=1，f（x+1）-f（x）=2x+5；函数g（x）=ax（a＞0且a≠1）（1）求f（x）的解析式；（2）若g（2）=14，且g[f（x）]≥k对x∈[-1，1]恒成立，求实数k的取值范围．

20．已知函数f（x）=loga（x-2a）+loga（x-3a）（a＞0且a≠1）．（1）当a=12，求f（2）的值；（2）当a=12时，若方程f（x）=log12（p-x）在（3，4）上有解，求实数p的取值范围；（3）若f（x）≤1在[a+3，a+4]上恒成立，求实数a的取值范围．

21．已知集合A={x|x2-4x-5≥0}，集合B={x|2a≤x≤a+2}．（1）若a=-1，求A∩B，A∪B；（2）若A∩B=B，求实数a的取值范围．

1．设a=log₅4，则
b
=
log
1
5
1
3
，c=0.5^-0.2，则a,b,c的大小关系是（　　）

3．已知集合M={x||x|＜3}，N={x|y=
6
+
x
-
x
2
}，则M∩N=（　　）

4．函数
f
（
x
）
=
2
x
2
-
2
x
，x∈[0，3]的值域是（　　）

5．已知函数y=f（x）在定义域（-1，1）上是减函数，且f（2a-1）＜f（1-a），则实数a的取值范围是（　　）

6．函数
y
=
x
-
1
+
lg
（
3
-
x
）
的定义域为（　　）

7．已知偶函数f（x）的定义域为R，当x∈[0，+∞）时，f（x）单调递增，则f（-2），f（π），f（-3）的大小关系是（　　）

8．下列函数中，在（0，+∞）上单调递增且值域为（0，+∞）的是（　　）

9．下列函数中是偶函数，且在区间（0，+∞）上是减函数的是（　　）

10．已知函数f（x）的导函数f'（x）的图象如图所示，则下列结论正确的是（　　）

11．已知幂函数f（x）=（m²-2m-2）x^m的图象过点
（
2
，
1
2
）
，则（　　）

12．下列说法正确的是（　　）

14．已知x＞0，y＞0，2xy=x+y+4，则x+y的最小值为
．

15．已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=log₂（2-x），则f（0）+f（2）=
．

16．用有理数指数幂的形式表示
a
a
=
．

18．已知定义在（-∞，0）∪（0，+∞）上的函数f（x）满足f（xy）+1=f（x）+f（y），且f（x）在（0，+∞）上单调递减．
（1）证明：函数f（x）是偶函数；
（2）解关于x的不等式f（x-1）+f（2）≥2．

19．已知函数f（x）是二次函数，且满足f（0）=1，f（x+1）-f（x）=2x+5；函数g（x）=a^x（a＞0且a≠1）
（1）求f（x）的解析式；
（2）若g（2）=
1
4
，且g[f（x）]≥k对x∈[-1，1]恒成立，求实数k的取值范围．

21．已知集合A={x|x²-4x-5≥0}，集合B={x|2a≤x≤a+2}．
（1）若a=-1，求A∩B，A∪B；
（2）若A∩B=B，求实数a的取值范围．