2023-2024学年陕西省西安八十五中九年级（上）开学数学试卷

一、选择题（每题3分，共30分）

• 1．下列方程是一元二次方程的是（　　）

  A．x+2y=1

  B．x+y2=1

  C．x- 2 x =1

  D．x2-2=0
  组卷：298引用：6难度：0.8

  解析

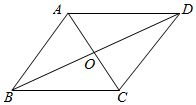• 2．如图，▱ABCD对角线AC，BD交于点O，请添加一个条件：____使得▱ABCD是菱形（　　）

  A．AB=AC

  B．AC⊥BD

  C．AB=CD

  D．AC=BD
  组卷：2271引用：16难度：0.7

  解析

• 3．用配方法解方程x²-6x+5=0，配方后可得（　　）

  A．（x-3）2=5

  B．（x-3）2=4

  C．（x-6）2=5

  D．（x-6）2=31
  组卷：528引用：7难度：0.7

  解析

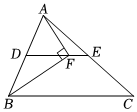• 4．如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF并延长交AC于点E．若AB=10，BC=16，则线段EF的长为（　　）

  A．5

  B．8

  C．3

  D．4
  组卷：180引用：3难度：0.6

  解析

• 5．若关于x的一元二次方程ax²+bx+1=0（a≠0）的一个解是x=1，则2022-a-b的值是（　　）

  A．2025

  B．2014

  C．2023

  D．2022
  组卷：215引用：5难度：0.5

  解析

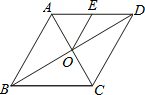• 6．如图，菱形ABCD的周长为24cm,对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长等于（　　）

  A．3cm

  B．4cm

  C．2.5cm

  D．2cm
  组卷：5137引用：28难度：0.9

  解析

• 7．根据下列表格的对应值，判断方程ax²+bx+c=0（a≠0，a,b,c为常数）的一个解x的范围是（　　）
  

  x	3.23	3.24	3.25	3.26
  ax2+bx+c	-0.06	-0.02	0.03	0.09

  A．3＜x＜3.23	B．3.23＜x＜3.24
  C．3.24＜x＜3.25	D．3.25＜x＜3.26
  组卷：1414引用：59难度：0.7

  解析

• 8．随着生产技术的进步，某制药厂生产成本逐年下降，两年前生产一吨药的成本是6000元，现在生产一吨药的成本是5000元．设生产成本的年平均下降为x,下列所列的方程正确的是（　　）

  A．6000（1+x）2=5000	B．5000（1+x）2=6000
  C．6000（1-x）2=5000	D．5000（1-x）2=6000
  组卷：1013引用：13难度：0.8

  解析

三、解答题（共9小题，共75分，解答题写过程）

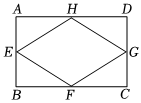• 23．如图，在矩形ABCD中，点E、F、G、H，分别是四边的中点．
  （1）判断四边形EFGH的形状，并给出理由；
  （2）当AB=6，AD=8时，四边形EFGH的面积等于

  ．
  组卷：23引用：2难度：0.5

  解析

• 24．我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用，例如：试求二次三项式x²+4x+5最小值．解：x²+4x+5=x²+4x+4+1=（x+2）²+1，∵（x+2）²≥0，（x+2）²+1≥1，∴x²+4x+5≥1，即x²+4x+5的最小值是1．试利用“配方法”解决下列问题：
  （1）已知y=x²-6x+12，求y的最小值．
  （2）比较代数式3x²-x+2与2x²+3x-6的大小，并说明理由．
  知识迁移：
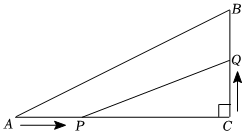
  （3）如图，在Rt△ABC中，∠C=90°，AC=4cm,BC=3cm,点P在AC边上以2cm/s的速度从点A向C移动，点Q在CB边上以1cm/s的速度从点C向点B移动．若点P，Q同时出发，且当一点移动到终点时，另一点也随之停止，设四边形APQB的面积为S cm²，运动时间为t秒，求S的最小值．
  组卷：768引用：5难度：0.2

  解析