当前位置：试卷中心 > 试卷详情

2023年广东省六校（广州二中、中山纪中、东莞中学、珠海一中、深圳实验、惠州一中）高考数学第六次联考试卷

发布：2025/11/5 22:0:38

一、单选题。（本题共8小题，每小题5分，共40分。在每小题的四个选项中，只有一项符合题目要求。）

1．下列函数在定义域中既是奇函数又是减函数的是（　　）
A．
y
=
1
x
B．y=-x|x| C．y=e^x-e^-x D．y=-lnx
组卷：193引用：5难度：0.8
2．已知复数z满足
iz
=
3
2
+
1
2
i
，则z²=（　　）
A．
1
2
+
3
2
i
B．
1
2
-
3
2
i
C．
-
1
2
-
3
2
i
D．
-
1
2
+
3
2
i
组卷：145引用：4难度：0.8
3．在三棱锥S-ABC中，三侧面两两互相垂直，侧面△SAB，△SBC，△SAC的面积分别为1，
3
2
，3，则此三棱锥的外接球的表面积为（　　）
A．14π B．12π C．10π D．8π
组卷：143引用：3难度：0.5
4．要做一个圆锥形的漏斗，其母线长为20cm,要使其体积最大，则高为（　　）
A．
3
3
B．
10
3
3
C．
16
3
3
D．
20
3
3
组卷：369引用：6难度：0.5
5．6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（　　）
A．60种 B．90种 C．120种 D．360种
组卷：390引用：12难度：0.7
6．已知全集为U，M∩N=M，则其图象为（　　）
A． B． C． D．
组卷：86引用：4难度：0.8
7．设
|
a
|
=
1
，
|
b
|
=
3
，且
a
⊥
b
，若向量
c
满足
|
c
-
a
-
b
|
=
2
|
a
-
b
|
，则
|
c
|
的最大值是（　　）
A．5 B．6 C．7 D．8
组卷：88引用：2难度：0.7
8．设
a
=
1
2
cos
5
°
-
3
2
sin
5
°
，
b
=
2
tan
13
°
1
+
tan
2
13
°
，
c
=
1
-
sin
42
°
2
，则a,b,c的大小关系正确的是（　　）
A．b＜a＜c B．c＜a＜b C．b＜c＜a D．c＜b＜a
组卷：119引用：6难度：0.7

二、多选题。（本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求。全部选对5分，部分选对得2分，有选错得0分。）

9．已知椭圆
C
：
x
2
9
+
y
2
8
=
1
的左、右焦点分别为F₁，F₂，点P为椭圆C的一个动点，点M（1，-1），则下列结论正确的是（　　）
A．存在点P，使得PF₁⊥PF₂
B．△PF₁F₂的面积最大值为
2
2
C．点P到直线
x
+
2
y
-
1
=
0
距离的最大值为
2
3
D．|PM|+|PF₁|的最大值为7
组卷：102引用：2难度：0.6
10．如图，在长方体ABCD-A₁B₁C₁D₁中，
AD
=
A
A
1
=
3
，AB=2，点P，E分别为AB，AA₁的中点，点M为直线CD₁上的动点，点N为直线C₁D₁上的动点，则（　　）
A．对任意的点N，一定存在点M，使得PM⊥DN
B．向量
PM
，
A
1
B
，
D
1
E
共面
C．异面直线PM和AA₁所成角的最小值为
π
4
D．存在点M，使得直线PM与平面DCC₁D₁所成角为
π
3
组卷：170引用：7难度：0.6

11．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，下列说法正确的是（　　）

A．

B．函数f（x）的图象关于直线

对称

C．函数f（x）图象向右平移

个单位可得函数y=2sin2x的图象

D．若方程f（x）=m（m∈R）在

[

，

]

上有两个不等实数根x₁，x₂，则

cos

（

）

组卷：46引用：3难度：0.6

12．已知函数f（x）=e^x+3（e是自然对数的底数），则下列结论正确的是（　　）

A．曲线y=f（x）的切线斜率可以是-1

B．曲线y=f（x）的切线斜率可以是2

C．过点（0，3）且与曲线y=f（x）相切的直线有且只有1条

D．过点（1，5）且与曲线y=f（x）相切的直线有且只有2条

组卷：30引用：1难度：0.5

三、填空题。

13．已知
（
x
2
-
2
x
）
n
的展开式的二项式系数之和为64，则展开式第三项的系数是
．
组卷：491引用：7难度：0.8
14．已知函数y=f（x）=x³+px²+qx的图象与x轴切于非原点的一点，那么p、q的关系为
．
组卷：19引用：1难度：0.7
15．计算
（
1
8
）
-
1
3
+
2
lo
g
2
3
-
lo
g
2
9
8
=
．
组卷：228引用：6难度：0.8
16．直线x+2y+1=0与圆x²+y²-4x+8y=0相交所得的弦长为
．
组卷：134引用：3难度：0.7

四、解答题。（本题共6小题，第17题10分，第18—22题各12分，共70分.解答应写出文字说明、证明过程或演算步骤.）

17．已知等差数列{a_n}满足：a_n+1=2a_n-2n+1，正项等比数列{b_n}满足：b₁=1，2b₁+b₂=b₃．
（1）求数列{a_n}、{b_n}的通项公式；
（2）求数列{b_n-a_n}的前10项和S₁₀．
组卷：32引用：1难度：0.5
18．已知⊙O₁：（x+1）²+y²=1，⊙O₂：（x-1）²+y²=9，⊙M与⊙O₁外切，与⊙O₂内切．
（1）求点M的轨迹方程；
（2）若A，B是点M的轨迹上的两点，O为坐标原点，直线OA，OB的斜率分别为k₁，k₂，直线AB的斜率存在，△AOB的面积为
3
，证明：k₁•k₂为定值．
组卷：91引用：5难度：0.5
19．△ABC的内角A，B，C的对边分别为a,b,c,已知2c-a=2bcosA．
（1）求角B的大小；
（2）若a=2，b=
7
，求c的长．
组卷：89引用：3难度：0.7
20．某年级有2000名学生．一次物理单元测验成绩近似服从正态分布X～N（72，8²）．
（1）求成绩不超过64分的人数占年级总人数的比例；
（2）估计全年级成绩在80～96分内的学生人数．
附：若X～N（μ，σ²），则P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973．
组卷：73引用：1难度：0.7
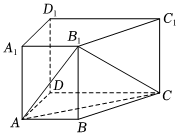21．如图，在四棱柱ABCD-A₁B₁C₁D₁中，侧棱AA₁垂直底面ABCD，AB∥DC，AA₁=1，AB=3k,AD=4k,BC=5k,DC=6k（k＞0）．
（1）求证：CD⊥平面ADD₁A₁．
（2）已知k=1，求二面角B₁-AC-B的大小．
（3）现将与四棱柱ABCD-A₁B₁C₁D₁形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成的新四棱柱中，记其中最小的表面积为f（k），写出f（k）的解析式．（直接写出答案，不必说明理由）．
组卷：9引用：1难度：0.6
22．已知f（e^x）=x-2e^x-3．
（1）求函数f（x）的解析式；
（2）求函数f（x）的值域；
（3）若函数
g
（
x
）
=
f
（
1
x
）
-
kx
在定义域上是增函数，求实数k的取值范围．
组卷：35引用：3难度：0.4

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2023年广东省六校（广州二中、中山纪中、东莞中学、珠海一中、深圳实验、惠州一中）高考数学第六次联考试卷

一、单选题。（本题共8小题，每小题5分，共40分。在每小题的四个选项中，只有一项符合题目要求。）

1．下列函数在定义域中既是奇函数又是减函数的是（ ）

2．已知复数z满足iz=32+12i，则z2=（ ）

3．在三棱锥S-ABC中，三侧面两两互相垂直，侧面△SAB，△SBC，△SAC的面积分别为1，32，3，则此三棱锥的外接球的表面积为（ ）

4．要做一个圆锥形的漏斗，其母线长为20cm,要使其体积最大，则高为（ ）

5．6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（ ）

6．已知全集为U，M∩N=M，则其图象为（ ）

7．设|a|=1，|b|=3，且a⊥b，若向量c满足|c-a-b|=2|a-b|，则|c|的最大值是（ ）

8．设a=12cos5°-32sin5°，b=2tan13°1+tan213°，c=1-sin42°2，则a,b,c的大小关系正确的是（ ）

二、多选题。（本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求。全部选对5分，部分选对得2分，有选错得0分。）

9．已知椭圆C：x29+y28=1的左、右焦点分别为F1，F2，点P为椭圆C的一个动点，点M（1，-1），则下列结论正确的是（ ）

10．如图，在长方体ABCD-A1B1C1D1中，AD=AA1=3，AB=2，点P，E分别为AB，AA1的中点，点M为直线CD1上的动点，点N为直线C1D1上的动点，则（ ）

11．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图象如图所示，下列说法正确的是（ ）

12．已知函数f（x）=ex+3（e是自然对数的底数），则下列结论正确的是（ ）

三、填空题。

13．已知（x2-2x）n的展开式的二项式系数之和为64，则展开式第三项的系数是 ．

14．已知函数y=f（x）=x3+px2+qx的图象与x轴切于非原点的一点，那么p、q的关系为．

15．计算（18）-13+2log23-log298=．

16．直线x+2y+1=0与圆x2+y2-4x+8y=0相交所得的弦长为 ．

四、解答题。（本题共6小题，第17题10分，第18—22题各12分，共70分.解答应写出文字说明、证明过程或演算步骤.）

17．已知等差数列{an}满足：an+1=2an-2n+1，正项等比数列{bn}满足：b1=1，2b1+b2=b3．（1）求数列{an}、{bn}的通项公式；（2）求数列{bn-an}的前10项和S10．

19．△ABC的内角A，B，C的对边分别为a,b,c,已知2c-a=2bcosA．（1）求角B的大小；（2）若a=2，b=7，求c的长．

22．已知f（ex）=x-2ex-3．（1）求函数f（x）的解析式；（2）求函数f（x）的值域；（3）若函数g（x）=f（1x）-kx在定义域上是增函数，求实数k的取值范围．

1．下列函数在定义域中既是奇函数又是减函数的是（　　）

2．已知复数z满足
iz
=
3
2
+
1
2
i
，则z²=（　　）

3．在三棱锥S-ABC中，三侧面两两互相垂直，侧面△SAB，△SBC，△SAC的面积分别为1，
3
2
，3，则此三棱锥的外接球的表面积为（　　）

4．要做一个圆锥形的漏斗，其母线长为20cm,要使其体积最大，则高为（　　）

5．6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（　　）

6．已知全集为U，M∩N=M，则其图象为（　　）

7．设
|
a
|
=
1
，
|
b
|
=
3
，且
a
⊥
b
，若向量
c
满足
|
c
-
a
-
b
|
=
2
|
a
-
b
|
，则
|
c
|
的最大值是（　　）

8．设
a
=
1
2
cos
5
°
-
3
2
sin
5
°
，
b
=
2
tan
13
°
1
+
tan
2
13
°
，
c
=
1
-
sin
42
°
2
，则a,b,c的大小关系正确的是（　　）

9．已知椭圆
C
：
x
2
9
+
y
2
8
=
1
的左、右焦点分别为F₁，F₂，点P为椭圆C的一个动点，点M（1，-1），则下列结论正确的是（　　）

10．如图，在长方体ABCD-A₁B₁C₁D₁中，
AD
=
A
A
1
=
3
，AB=2，点P，E分别为AB，AA₁的中点，点M为直线CD₁上的动点，点N为直线C₁D₁上的动点，则（　　）

11．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，下列说法正确的是（　　）

12．已知函数f（x）=e^x+3（e是自然对数的底数），则下列结论正确的是（　　）

13．已知
（
x
2
-
2
x
）
n
的展开式的二项式系数之和为64，则展开式第三项的系数是
．

14．已知函数y=f（x）=x³+px²+qx的图象与x轴切于非原点的一点，那么p、q的关系为
．

15．计算
（
1
8
）
-
1
3
+
2
lo
g
2
3
-
lo
g
2
9
8
=
．

16．直线x+2y+1=0与圆x²+y²-4x+8y=0相交所得的弦长为
．

17．已知等差数列{a_n}满足：a_n+1=2a_n-2n+1，正项等比数列{b_n}满足：b₁=1，2b₁+b₂=b₃．
（1）求数列{a_n}、{b_n}的通项公式；
（2）求数列{b_n-a_n}的前10项和S₁₀．

19．△ABC的内角A，B，C的对边分别为a,b,c,已知2c-a=2bcosA．
（1）求角B的大小；
（2）若a=2，b=
7
，求c的长．

22．已知f（e^x）=x-2e^x-3．
（1）求函数f（x）的解析式；
（2）求函数f（x）的值域；
（3）若函数
g
（
x
）
=
f
（
1
x
）
-
kx
在定义域上是增函数，求实数k的取值范围．