2022-2023学年浙江省金华市义乌市江东中学九年级（上）期中数学试卷

一、选择题（每小题3分，共30分）

• 1．抛物线y=2（x-1）²+3的顶点坐标是（　　）

  A．（1，3）

  B．（1，-3）

  C．（-1，3）

  D．（-1，-3）
  组卷：448引用：18难度：0.9

  解析

• 2．将抛物线y=x²-2向左平移1个单位后所得新抛物线的表达式为（　　）

  A．y=x2-1

  B．y=x2-3

  C．y=（x+1）2-2

  D．y=（x-1）2-2
  组卷：49引用：3难度：0.6

  解析

• 3．已知⊙O的半径为2cm,点P到圆心O的距离为4cm,则点P和⊙O的位置关系为（　　）

  A．点P在圆内

  B．点P在圆上

  C．点P在圆外

  D．不能确定
  组卷：428引用：12难度：0.6

  解析

• 4．如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是（　　）

  A．（1，1）

  B．（1，2）

  C．（1，3）

  D．（1，4）
  组卷：3356引用：121难度：0.7

  解析

• 5．在一个不透明的口袋里装有2个白球和3个红球，它们除颜色外其余都相同，现随机从袋里摸出1个球，则摸出白球的概率是（　　）

  A． 1 2

  B． 2 3

  C． 2 5

  D． 3 5
  组卷：20引用：3难度：0.6

  解析

• 6．如图，A，B，C是⊙O上的点，满足CA平分∠OCB．若∠OAC=25°，则∠AOB的度数为（　　）

  A．40°

  B．50°

  C．55°

  D．60°
  组卷：324引用：2难度：0.7

  解析

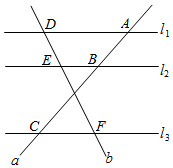• 7．如图，直线l₁∥l₂∥l₃，直线a、b与l₁、l₂、l₃分别交于点A、B、C和点D、E、F，若AB：BC=1：2，DE=2，则EF的长为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：1184引用：12难度：0.9

  解析

• 8．若二次函数y=x²-6x+9的图象经过A（-1，y₁），B（1，y₂），C（3+

  3

  ，y₃）三点．则关于y₁，y₂，y₃大小关系正确的是（　　）

  A．y1＞y2＞y3

  B．y1＞y3＞y2

  C．y2＞y1＞y3

  D．y3＞y1＞y2
  组卷：659引用：12难度：0.7

  解析

三、解答题（本题有8小题，第17～19圈每题6分，第20、21每8分，第22、23每题10分，第24小圈12分，共66分）

• 23．如图1，正方形ABCD的边长为6，E是AD边上一点（不含端点），连接CE，P是D点关于EC的对称点，连接PA，PB，PC，PE．CH平分∠PCB交AB于点H，G为CE中点，连接PH，PG．设ED的长为a.
  
  （1）则∠HPC的度数为

  ．
  （2）如图2，当点P恰好落在线段AG上时，求证：△AEP∽△AGE；
  （3）是否存在a的值，使得PG与△HBC的一边平行，若存在，求出所有满足要求的a的值：若不存在，请说明理由．
  组卷：17引用：2难度：0.1

  解析

• 24．如图1，抛物线y=a（x+2）（x-6）（a＞0）与x轴交于C，D两点（点C在点D的左边），与y轴负半轴交于点A．
  （1）若△ACD的面积为16．
  ①求抛物线解析式；
  ②S为线段OD上一点，过S作x轴的垂线，交抛物线于点P，将线段SC，SP绕点S顺时针旋转任意相同的角到SC₁，SP₁的位置，使点C，P的对应点C₁，P₁都在x轴上方，C₁C与P₁S交于点M，P₁P与x轴交于点N．求

  SN

  SM

  的最大值；
  （2）如图2，直线y=x-12a与x轴交于点B，点M在抛物线上，且满足∠MAB=75°的点M有且只有两个，求a的取值范围．
  
  组卷：779引用：5难度：0.3

  解析