当前位置：试卷中心 > 试卷详情

2024-2025学年四川省眉山中学高二（上）期末数学试卷

发布：2025/11/4 6:0:31

一、单选题

1．直线2x+6y-1=0的方向向量为（　　）
A．（3，1） B．（1，-3） C．（1，3） D．（3，-1）
组卷：333引用：1难度：0.8
2．已知F₁，F₂分别为双曲线
x
2
2
-
y
2
6
=
1
的左，右焦点，直线l过点F₂，且与双曲线右支交于A，B两点，O为坐标原点，△AF₁F₂，△BF₁F₂的内切圆的圆心分别为O₁，O₂，则△OO₁O₂面积的取值范围是（　　）
A．
（
2
，
4
3
3
）
B．
[
2
，
4
3
3
）
C．
[
2
，
4
3
3
）
∪
（
4
3
3
，
+
∞
）
D．
[
2
，
2
6
3
]
组卷：209引用：3难度：0.6
3．据统计，下午2点在某超市付款处排队的人数及其概率如下表，则下午2点至多有2人排队的概率为（　　）

排队人数 0 1 2 3 4 5人及以上

概率 0.1 0.25 0.31 0.2 0.1 0.04

A．0.31 B．0.34 C．0.35 D．0.66
组卷：77引用：1难度：0.8
4．从集合{0，1，2，3}中随机地取一个数a,从集合{2，4，6}中随机地取一个数b,则向量
m
=（a,b）与
n
=（1，2）平行的概率为（　　）
A．
1
2
B．
1
3
C．
1
4
D．
1
6
组卷：2引用：1难度：0.7
5．已知 M（-2，0），圆C：x²-4x+y²=0，动圆P经过M点且与圆C相切，则动圆圆心P的轨迹方程是（　　）
A．x²-
y
2
3
=1（x≥1） B．
x
2
3
-y²=1（x≥
3
）
C．x²-
y
2
3
=1 D．
x
2
3
-y²=1
组卷：118引用：2难度：0.7
6．双曲线
x
2
a
2
-
y
2
12
=
1
（
a
＞
0
）
的两个焦点分别是F₁和F₂，焦距为8；M是双曲线上的一点，且|MF₁|=5，则|MF₂|的值为（　　）
A．1 B．4 C．9 D．1或9
组卷：623引用：12难度：0.7
7．如图，AB=AC=BD=1，AB⊂平面α，AC⊥平面α，BD⊥AB，BD与平面α成30°角，则C，D间的距离为（　　）
A．1 B．2 C．
2
D．
3
组卷：40引用：2难度：0.5
8．系统找不到该试题

二、多选题

9．已知双曲线C：x²-
y
2
3
=1，F₁，F₂为双曲线的左、右焦点，若直线l过点F₂，且与双曲线的右支交于M，N两点，下列说法正确的是（　　）
A．双曲线C的离心率为
3
B．若l的斜率为2，则MN的中点为（8，12）
C．若∠F₁MF₂=
π
3
，则△MF₁F₂的面积为3
3
D．使△MNF₁为等腰三角形的直线l有3条
组卷：7引用：0难度：0.5

10．某市为丰富青少年憵假生活，推出多项益智游乐项目．小乐与好朋友一起选择了该市的甲、乙两个儿童乐园游乐场去打卡．小乐与好朋友第一天去甲、乙两家游乐场游玩的概率分别为0.3和0.7．如果他们第一天去甲游乐场，那么第二天去甲游乐场的概率为0.7；如果第一天去乙游乐场，那么第二天去甲游乐场的概率为0.6，则小乐与好朋友（　　）

A．第二天去甲游乐场的概率为0.63

B．第二天去乙游乐场的概率为0.45

C．第二天去了甲游乐场，则第一天去乙游乐场的概率为

D．第二天去了乙游乐场，则第一天去甲游乐场的概率为

组卷：45引用：3难度：0.8

11．在
（
x
+
1
x
）
9
的展开式中，下列结论正确的是（　　）
A．第6项和第7项的二项式系数相等
B．奇数项的二项式系数和为256
C．常数项为84
D．有理项有2项
组卷：246引用：11难度：0.7

三、填空题

12．已知抛物线y²=2px（p＞0），过焦点F的直线与抛物线交于M，N两点（点M在第一象限）．若直线MN的斜率为
3
，点M的横坐标为6，则p=
．
组卷：7引用：1难度：0.6
13．已知椭圆
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）和双曲线
x
2
m
2
-
y
2
n
2
=1（m＞0，n＞0）有相同的焦点F₁，F₂，P为椭圆与双曲线的一个公共点，椭圆与双曲线的离心率分别为e₁，e₂，∠F₁PF₂=
π
3
，且e₂∈[
2
，
3
]，则e₁的取值范围为
．
组卷：147引用：5难度：0.6
14．已知随机事件A、B相互独立，若
P
（
A
）
=
3
4
，
P
（
B
）
=
2
3
，则P（A∩B）=
．
组卷：136引用：8难度：0.7

四、解答题

15．同一种产品由甲、乙、丙三个厂供应．由长期的经验知，三家的正品率分别为0.95，0.90，0.80，三家产品数所占比例为2：3：5，混合在一起．
（1）从中任取一件，求此产品为正品的概率；
（2）现取到一件产品为正品，问它是由甲、乙、丙三个厂中哪个厂生产的可能性最大？
组卷：179引用：4难度：0.7
16．已知圆C的圆心在直线2x+y-4=0上，且与y轴相切于点O（0，0）．
（1）求圆C的方程；
（2）已知过点P（1，3）的直线l被圆C截得的弦长为
2
3
，求直线l的方程．
组卷：197引用：3难度：0.5
17．已知抛物线的顶点在原点，焦点与椭圆4x²+5y²=20的一个焦点相同，
（1）求椭圆的焦点坐标与离心率；
（2）求抛物线方程．
组卷：11引用：1难度：0.5
18．已知椭圆C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）经过点M（1，
2
2
），N（
2
，0）．
（1）求椭圆C的方程；
（2）已知直线l的倾斜角为锐角，l与圆x²+y²=
1
2
相切，与椭圆C交于A、B两点，且△AOB的面积为
2
3
，求直线l的方程．
组卷：266引用：3难度：0.6
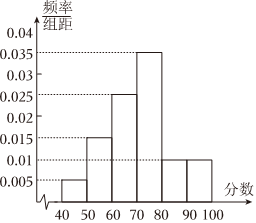19．某学校高一100名学生参加数学竞赛，成绩均在40分到100分之间．学生成绩的频率分布直方图如图：
（Ⅰ）估计这100名学生分数的中位数；（精确到0.1）
（Ⅱ）某老师抽取了10名学生的分数：x₁，x₂，x₃⃯，…，x₁₀，已知这10个分数的平均数
x
=
90
，标准差s=6，若剔除其中的100和80两个分数，求剩余8个分数的平均数与标准差；
（Ⅲ）该学校有3座构造相同教学楼，各教学楼高均为20米，东西长均为60米，南北宽均为20米．其中1号教学楼在2号教学楼的正南且楼距为40米，3号教学楼在2号教学楼的正东且楼距为72米．现有3种型号的考试屏蔽仪，它们的信号覆盖半径依次为35，55，105米，每个售价相应依次为1500，2000，4000元．若屏蔽仪可在地下及地上任意位置安装且每个安装费用均为100元，求让各教学楼均被屏蔽仪信号完全覆盖的最小花费．
（参考公式：
s
=
n
∑
i
=
1
x
2
i
-
n
x
2
n
，参考数据：210²=44100，192²=36864，110²=12100）
组卷：21引用：1难度：0.7

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．（ 2 ， 4 3 3 ）	B． [ 2 ， 4 3 3 ）
C． [ 2 ， 4 3 3 ） ∪ （ 4 3 3 ， + ∞ ）	D． [ 2 ， 2 6 3 ]

A．x²- y 2 3 =1（x≥1）	B． x 2 3 -y²=1（x≥ 3 ）
C．x²- y 2 3 =1	D． x 2 3 -y²=1

排队人数	0	1	2	3	4	5人及以上
概率	0.1	0.25	0.31	0.2	0.1	0.04

2024-2025学年四川省眉山中学高二（上）期末数学试卷

一、单选题

1．直线2x+6y-1=0的方向向量为（ ）

2．已知F1，F2分别为双曲线x22-y26=1的左，右焦点，直线l过点F2，且与双曲线右支交于A，B两点，O为坐标原点，△AF1F2，△BF1F2的内切圆的圆心分别为O1，O2，则△OO1O2面积的取值范围是（ ）

3．据统计，下午2点在某超市付款处排队的人数及其概率如下表，则下午2点至多有2人排队的概率为（ ） 排队人数 0 1 2 3 4 5人及以上 概率 0.1 0.25 0.31 0.2 0.1 0.04

4．从集合{0，1，2，3}中随机地取一个数a,从集合{2，4，6}中随机地取一个数b,则向量m=（a,b）与n=（1，2）平行的概率为（ ）

5．已知 M（-2，0），圆C：x2-4x+y2=0，动圆P经过M点且与圆C相切，则动圆圆心P的轨迹方程是（ ）

6．双曲线x2a2-y212=1（a＞0）的两个焦点分别是F1和F2，焦距为8；M是双曲线上的一点，且|MF1|=5，则|MF2|的值为（ ）

7．如图，AB=AC=BD=1，AB⊂平面α，AC⊥平面α，BD⊥AB，BD与平面α成30°角，则C，D间的距离为（ ）

二、多选题

9．已知双曲线C：x2-y23=1，F1，F2为双曲线的左、右焦点，若直线l过点F2，且与双曲线的右支交于M，N两点，下列说法正确的是（ ）

11．在（x+1x）9的展开式中，下列结论正确的是（ ）

三、填空题

12．已知抛物线y2=2px（p＞0），过焦点F的直线与抛物线交于M，N两点（点M在第一象限）．若直线MN的斜率为3，点M的横坐标为6，则p=．

13．已知椭圆x2a2+y2b2=1（a＞b＞0）和双曲线x2m2-y2n2=1（m＞0，n＞0）有相同的焦点F1，F2，P为椭圆与双曲线的一个公共点，椭圆与双曲线的离心率分别为e1，e2，∠F1PF2=π3，且e2∈[2，3]，则e1的取值范围为 ．

14．已知随机事件A、B相互独立，若P（A）=34，P（B）=23，则P（A∩B）=．

四、解答题

16．已知圆C的圆心在直线2x+y-4=0上，且与y轴相切于点O（0，0）．（1）求圆C的方程；（2）已知过点P（1，3）的直线l被圆C截得的弦长为23，求直线l的方程．

17．已知抛物线的顶点在原点，焦点与椭圆4x2+5y2=20的一个焦点相同，（1）求椭圆的焦点坐标与离心率；（2）求抛物线方程．

18．已知椭圆C：x2a2+y2b2=1（a＞b＞0）经过点M（1，22），N（2，0）．（1）求椭圆C的方程；（2）已知直线l的倾斜角为锐角，l与圆x2+y2=12相切，与椭圆C交于A、B两点，且△AOB的面积为23，求直线l的方程．

1．直线2x+6y-1=0的方向向量为（　　）

2．已知F₁，F₂分别为双曲线
x
2
2
-
y
2
6
=
1
的左，右焦点，直线l过点F₂，且与双曲线右支交于A，B两点，O为坐标原点，△AF₁F₂，△BF₁F₂的内切圆的圆心分别为O₁，O₂，则△OO₁O₂面积的取值范围是（　　）

3．据统计，下午2点在某超市付款处排队的人数及其概率如下表，则下午2点至多有2人排队的概率为（　　）

排队人数 0 1 2 3 4 5人及以上

概率 0.1 0.25 0.31 0.2 0.1 0.04

4．从集合{0，1，2，3}中随机地取一个数a,从集合{2，4，6}中随机地取一个数b,则向量
m
=（a,b）与
n
=（1，2）平行的概率为（　　）

5．已知 M（-2，0），圆C：x²-4x+y²=0，动圆P经过M点且与圆C相切，则动圆圆心P的轨迹方程是（　　）

6．双曲线
x
2
a
2
-
y
2
12
=
1
（
a
＞
0
）
的两个焦点分别是F₁和F₂，焦距为8；M是双曲线上的一点，且|MF₁|=5，则|MF₂|的值为（　　）

7．如图，AB=AC=BD=1，AB⊂平面α，AC⊥平面α，BD⊥AB，BD与平面α成30°角，则C，D间的距离为（　　）

9．已知双曲线C：x²-
y
2
3
=1，F₁，F₂为双曲线的左、右焦点，若直线l过点F₂，且与双曲线的右支交于M，N两点，下列说法正确的是（　　）

11．在
（
x
+
1
x
）
9
的展开式中，下列结论正确的是（　　）

12．已知抛物线y²=2px（p＞0），过焦点F的直线与抛物线交于M，N两点（点M在第一象限）．若直线MN的斜率为
3
，点M的横坐标为6，则p=
．

14．已知随机事件A、B相互独立，若
P
（
A
）
=
3
4
，
P
（
B
）
=
2
3
，则P（A∩B）=
．

16．已知圆C的圆心在直线2x+y-4=0上，且与y轴相切于点O（0，0）．
（1）求圆C的方程；
（2）已知过点P（1，3）的直线l被圆C截得的弦长为
2
3
，求直线l的方程．

17．已知抛物线的顶点在原点，焦点与椭圆4x²+5y²=20的一个焦点相同，
（1）求椭圆的焦点坐标与离心率；
（2）求抛物线方程．

18．已知椭圆C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）经过点M（1，
2
2
），N（
2
，0）．
（1）求椭圆C的方程；
（2）已知直线l的倾斜角为锐角，l与圆x²+y²=
1
2
相切，与椭圆C交于A、B两点，且△AOB的面积为
2
3
，求直线l的方程．