2023-2024学年湖北省荆州市沙市中学高二（上）月考数学试卷（9月份）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．用简单随机抽样的方法从含有10个个体的总体中，抽取一个容量为3的样本，其中某一个体a“第一次被抽到”的可能性，“第二次被抽到”的可能性分别是（　　）

  A． 1 10 ， 1 10

  B． 3 10 ， 1 5

  C． 1 5 ， 3 10

  D． 3 10 ， 3 10
  组卷：1055引用：17难度：0.9

  解析

• 2．已知{

  a

  ，

  b

  ，

  c

  }为空间的一组基底，则下列向量也能作为空间的一组基底的是（　　）

  A． a + b ， b + c ， a - c	B． a +2 b ， b ， a + c
  C．2 a + b ， b +2 c ， a + b + c	D． a + c ， b +2 a ， b -2 c
  组卷：104引用：6难度：0.8

  解析

• 3．已知两个向量

  a

  =

  （

  2

  ，-

  1

  ，

  3

  ）

  ，

  b

  =

  （

  4

  ，

  m

  ,

  n

  ）

  ，且

  a

  ∥

  b

  ，则m+n的值为（　　）

  A．1

  B．2

  C．4

  D．8
  组卷：488引用：29难度：0.9

  解析

• 4．已知向量

  a

  =

  （

  2

  3

  ，

  0

  ，

  2

  ）

  ，向量

  b

  =

  （

  1

  2

  ，

  0

  ，

  3

  2

  ）

  ，则向量

  a

  在向量

  b

  上的投影向量为（　　）

  A． （ 3 ， 0 ， 3 ）

  B． （ - 3 ， 0 ， 1 ）

  C． （ 1 ， 0 ， 3 ）

  D． （ 1 4 ， 0 ， 3 4 ）
  组卷：287引用：14难度：0.9

  解析

• 5．如图，元件A_i（i=1，2，3，4）通过电流的概率均为0.9，且各元件是否通过电流相互独立，则电流能在M，N之间通过的概率是（　　）

  A．0.729

  B．0.8829

  C．0.864

  D．0.9891
  组卷：1116引用：10难度：0.9

  解析

• 6．同时抛掷两颗骰子，观察向上的点数，记事件A=“点数之和为7”，事件B=“点数之和为3的倍数”，则（　　）

  A．A+B为不可能事件	B．A与B为互斥事件
  C．AB为必然事件	D．A与B为对立事件
  组卷：108引用：3难度：0.8

  解析

• 7．袋子里装有形状大小完全相同的4个小球，球上分别标有数字1，2，3，4，从中有放回的随机取两次，每次取1个球，A表示事件“第一次取出的球上数字是1”，B表示事件“第二次取出的球上数字是2”，C表示事件“两次取出的球上数字之和是5”，D表示事件“两次取出的球上数字之和是6”，通过计算，则可以得出（　　）

  A．B与D相互独立	B．A与D相互独立
  C．B与C相互独立	D．C与D相互独立
  组卷：167引用：7难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．

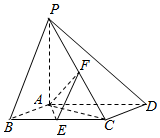• 21．如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
  （1）证明：AE⊥PD；
  （2）若H为PD上的动点，EH与平面PAD所成最大角的正弦值为

  15

  5

  ，求二面角E-AF-C的余弦值．
  组卷：216引用：3难度：0.5

  解析

• 22．如图，在矩形ABCD中，AB=1，

  BC

  =

  3

  ，M是线段AD上的一动点，将△ABM沿着BM折起，使点A到达点A′的位置，满足点A′∉平面BCDM且点A′在平面BCDM内的射影E落在线段BC上．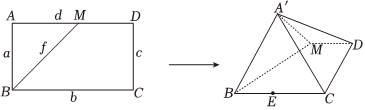
  
  （1）当点M与端点D重合时，证明：A′B⊥平面A′CD；
  （2）求三棱锥E-A′BM的体积的最大值；
  （3）设直线CD与平面A′BM所成的角为α，二面角A′-BM-C的平面角为β、求sin²α•cosβ的最大值．
  组卷：239引用：4难度：0.5

  解析