2023-2024学年辽宁省沈阳市新民高级中学高三（上）月考数学试卷（10月份）

一．选择题（共8小题每题5分）

• 1．已知集合A={x|x²≤4x}，B={x|3x-4＞0}，则A∩B=（　　）

  A．（-∞，0）

  B．[0， 4 3 ）

  C．（ 4 3 ，4]

  D．（-∞，0）
  组卷：96引用：6难度：0.9

  解析

• 2．若复数z满足（1+2i）•z=3+4i（其中i是虚数单位），复数z的共轭复数为

  z

  ，则（　　）

  A．z的实部是 11 5

  B．z的虚部是 2 5

  C．复数 z 在复平面内对应的点在第四象限

  D．|z|=5
  组卷：101引用：4难度：0.7

  解析

• 3．已知数列{a_n}是等差数列，数列{b_n}是等比数列，

  a

  7

  +

  a

  9

  =

  4

  π

  3

  ，且b₂b₆b₁₀=8，

  a

  3

  +

  a

  8

  +

  a

  13

  b

  4

  b

  8

  -

  1

  =（　　）

  A． π 4

  B． π 3

  C． π 2

  D． 2 π 3
  组卷：199引用：8难度：0.7

  解析

• 4．函数y=

  sin

  2

  x

  1

  -

  cosx

  的部分图象大致为（　　）

  A．	B．
  C．	D．
  组卷：7587引用：48难度：0.7

  解析

• 5．已知a=log₅2，b=log_0.50.2，c=0.5^0.2，则a,b,c的大小关系为（　　）

  A．a＜c＜b

  B．a＜b＜c

  C．b＜c＜a

  D．c＜a＜b
  组卷：6995引用：55难度：0.7

  解析

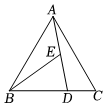• 6．如图，△ABC是边长为3的等边三角形，D在线段BC上，且

  BD

  =2

  DC

  ，E为线段AD上一点，若△ABE与△ACD的面积相等，则

  BE

  •

  AC

  的值为（　　）

  A． 1 4

  B．- 1 4

  C． 3 4

  D．- 3 4
  组卷：365引用：6难度：0.6

  解析

• 7．在△ABC中，角A，B，C所对的边分别为a,b,c,∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为（　　）

  A．8

  B．9

  C．10

  D．7
  组卷：1069引用：6难度：0.7

  解析

四、解答题（共6小题17题10分其余每题12分）

• 21．已知递增数列{a_n}的前n项和为S_n，且

  2

  S

  n

  =

  a

  n

  2

  +

  n

  ，数列{b_n}满足b₁=a₁，b₄=4a₂，

  b

  n

  b

  n

  +

  2

  =

  b

  2

  n

  +

  1

  ，

  n

  ∈

  N

  *

  ．
  （1）求数列{a_n}和{b_n}的通项公式；
  （2）记

  c

  n

  =

  （ 6 n - 7 ） b n 8 S n - 3 ， n 为奇数

  lo g 2 b n + 1 ， n 为偶数

  ，数列{c_n}的前2n项和为T_2n，若不等式

  （

  -

  1

  ）

  n

  λ

  +

  4

  n

  4

  n

  +

  1

  ＜

  T

  2

  n

  对一切n∈N^*恒成立，求λ的取值范围．
  组卷：276引用：3难度：0.3

  解析

• 22．已知函数f（x）=e^x•cosx-sinx-1（e为自然对数的底数）．
  （1）证明：当

  x

  ∈

  [

  0

  ，

  π

  2

  ]

  时，f（x）≤0；
  （2）证明：f（x）在区间（0，5π）内有4个零点；
  （3）记（2）中的4个零点为x₁，x₂，x₃，x₄，且x₁＜x₂＜x₃＜x₄，求证：x₁+x₄＞x₂+x₃．
  组卷：95引用：2难度：0.6

  解析