2022-2023学年辽宁省辽南协作校高一(下)期末数学试卷
发布:2024/6/27 8:0:9
一、单项选择题(本题共8小题,每小题5分,共40分.每小题只有一个选项符合要求)
-
1.已知
,则|z|=( )z=15+75i组卷:18引用:1难度:0.8 -
2.若向量
,a=(1,x),且b=(3,-1),a的夹角为45°,则x的值为( )b组卷:66引用:2难度:0.7 -
3.已知复数z=i5(1+i),则z在复平面内对应的点位于( )
组卷:40引用:3难度:0.8 -
4.关于直线l,m及平面α,β,下列命题正确的是( )
组卷:29引用:1难度:0.6 -
 5.斛是我国古代的一种量器,如图所示的斛可视为正四棱台,若该正四棱台的上、下底面边长分别为,22,侧面积为72,则该正四棱台的体积为( )42组卷:107引用:4难度:0.5
5.斛是我国古代的一种量器,如图所示的斛可视为正四棱台,若该正四棱台的上、下底面边长分别为,22,侧面积为72,则该正四棱台的体积为( )42组卷:107引用:4难度:0.5 -
6.已知角α为锐角,角α,2α,α+θ(0<θ<α)的始边均与x轴的正半轴重合,角α的终边经过点P(3,4),且角α的终边与角2α的终边关于角(α+θ)的终边对称,则tan(α+θ)=( )
组卷:52引用:1难度:0.7 -
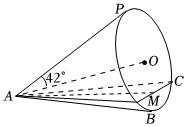 7.用数学的眼光观察世界,神奇的彩虹角约为42°,如图,眼睛与彩虹之间可以抽象为一个圆锥,设AO是眼睛与彩虹中心的连线,AP是眼睛与彩虹最高点的连线,则称∠OAP为彩虹角.若平面ABC为水平面,BC为彩虹面与水平面的交线,M为BC的中点,BC=600米,AM=400米,则彩虹的长度约为( )(ˆBPC)
7.用数学的眼光观察世界,神奇的彩虹角约为42°,如图,眼睛与彩虹之间可以抽象为一个圆锥,设AO是眼睛与彩虹中心的连线,AP是眼睛与彩虹最高点的连线,则称∠OAP为彩虹角.若平面ABC为水平面,BC为彩虹面与水平面的交线,M为BC的中点,BC=600米,AM=400米,则彩虹的长度约为( )(ˆBPC)
(参考数据:sin42°≈0.67,sin1.1≈)6067组卷:39引用:2难度:0.5
四、解答题(本大题共6小题,共70分,解答需写出文字说明、证明过程或演算步骤)
-
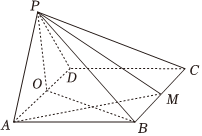 21.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,AB=PA=PD=2,O为AD的中点.
21.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,AB=PA=PD=2,O为AD的中点.
(1)证明:BC⊥平面POB;
(2)若为线段BC上一点(不包括端点),PB=6,M,四棱锥P-OMCD的体积为BM=λBC,求λ的值.1312组卷:75引用:1难度:0.5 -
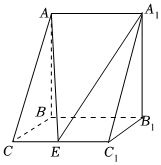 22.如图,三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知∠BCC1=C=2,点E是棱C1C的中点.π3,BC=1,AB=C1
22.如图,三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知∠BCC1=C=2,点E是棱C1C的中点.π3,BC=1,AB=C1
(1)求证:C1B⊥AC;
(2)求BA1与平面A1B1E所成角的正弦值.组卷:110引用:1难度:0.5


