2022-2023学年广东省江门市台山一中高二(上)期中数学试卷
发布:2024/9/5 8:0:8
一、单选题(本大题共8小题,共40分。)
-
1.经过点(1,2),且斜率为2的直线方程是( )
组卷:21引用:1难度:0.9 -
2.已知空间向量
,a=(2,-3,4),m,n∈R,若b=(-4,m,n),则m-n=( )a∥b组卷:295引用:8难度:0.7 -
3.已知椭圆
+x2a2=1(a>b>0)的离心率为y2b2,直线2x+y+10=0过椭圆的左顶点,则椭圆方程为( )35组卷:505引用:6难度:0.8 -
4.在△ABC中,AD为BC边上的中线,E为AD的中点,则
=( )EB组卷:17695引用:172难度:0.9 -
5.设A(2,-1),B(4,1),则以线段AB为直径的圆的方程是( )
组卷:1997引用:12难度:0.9 -
6.设双曲线
的左、右焦点分别为F1,F2,离心率为C:x2a2-y2b2=1(a>0,b>0),P是双曲线C上一点,且∠F1PF2=60°.若△F1PF2的面积为3,则△F1PF2的周长为( )43组卷:564引用:5难度:0.5 -
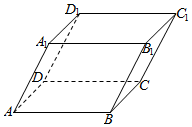 7.如图所示,在平行六面体ABCD-A'B'C'D'中,AB=1,AD=2,AA′=3,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC'的长为( )组卷:87引用:4难度:0.6
7.如图所示,在平行六面体ABCD-A'B'C'D'中,AB=1,AD=2,AA′=3,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC'的长为( )组卷:87引用:4难度:0.6
四、解答题(本大题共6小题,共70分。解答写出文字说明,证明过程,演算步骤)
-
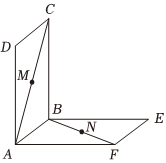 21.如图,边长为1的正方形ABCD所在平面与正方形ABEF所在平面互相垂直,动点M、N分别在正方形对角线AC和BF上移动,且.CM=BN=a(0<a<2)
21.如图,边长为1的正方形ABCD所在平面与正方形ABEF所在平面互相垂直,动点M、N分别在正方形对角线AC和BF上移动,且.CM=BN=a(0<a<2)
(1)求证MN与平面BCE平行;
(2)当时,求二面角A-MN-B的余弦值.a=22组卷:12引用:2难度:0.5 -
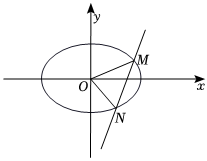 22.已知椭圆的离心率为C:x2a2+y2b2=1(a>b>0),且经过点12.P(1,32)
22.已知椭圆的离心率为C:x2a2+y2b2=1(a>b>0),且经过点12.P(1,32)
(1)求椭圆C的方程;
(2)若直线y=kx+m与椭圆C交于M、N两点,O为坐标原点,直线OM、ON的斜率之积等于,试探求△OMN的面积是否为定值,并说明理由.-34组卷:61引用:2难度:0.5


