2022-2023学年江西省南昌市青山湖区雷式学校八年级（下）期中数学试卷

一、单选题（每题3分，共18分）

• 1．若

  3

  =a,

  30

  =b,则

  0

  .

  9

  =（　　）

  A． a 10 b

  B． b 10 a

  C． ab 10

  D． a + b 10
  组卷：296引用：10难度：0.7

  解析

• 2．若实数k、b满足k+b=0，且k＞b,则一次函数y=kx+b的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：2940引用：7难度：0.7

  解析

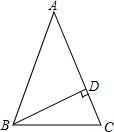• 3．已知如图，在△ABC中，AB=AC=10，BD⊥AC于D，CD=2，则BD的长为（　　）

  A．4

  B．5

  C．6

  D．8
  组卷：328引用：7难度：0.9

  解析

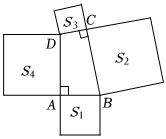• 4．如图，在四边形ABCD中，∠DAB=∠BCD=90°，分别以四边形的四条边为边向外作四个正方形，若S₁+S₄=80，S₃=30，则S₂=（　　）

  A．120

  B．110

  C．50

  D．40
  组卷：271引用：3难度：0.5

  解析

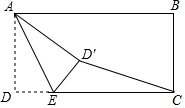• 5．如图，矩形ABCD中，AB=4，BC=2，把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处，则CD′的最小值是（　　）

  A．2

  B． 5

  C． 2 5 - 2

  D． 2 5 + 2
  组卷：786引用：3难度：0.7

  解析

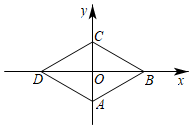• 6．如图，已知菱形ABCD的顶点A（0，-1），∠DAC=60°．若点P从点A出发，沿A→B→C→D→A…的方向，在菱形的边上以每秒0.5个单位长度的速度移动，则第2020秒时，点P的坐标为（　　）

  A．（2，0）

  B．（ 3 ，0）

  C．（- 3 ，0）

  D．（0，1）
  组卷：997引用：4难度：0.5

  解析

二、填空题（每题3分，共18分）

• 7．若函数y=（m+1）x^|m|-1-3是关于x的一次函数，且y随x的增大而减小，则m=

  ．
  组卷：270引用：3难度：0.7

  解析

五、解答题（每题9分，共18分）

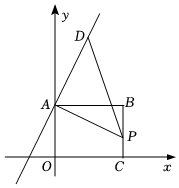• 22．已知长方形ABCO，O为坐标原点，B的坐标为（8，6），点A，C分别在坐标轴上，P是线段BC上的动点，设PC=m,
  （1）已知点D在第一象限且是直线y=2x+6上的一点，设D点横坐标为n,则D点纵坐标可用含n的代数式表示为

  ，此时若△APD是等腰直角三角形，求点D的坐标；
  （2）直线y=2x+b过点（3，0），请问在该直线上，是否存在第一象限的点D使△APD是等腰直角三角形？若存在，请直接写出这些点的坐标，若不存在，请说明理由．
  组卷：2877引用：6难度：0.3

  解析

六、解答题（共12分）

• 23．问题：如图1，P是矩形ABCD内任意一点，通过构造直角三角形，利用勾股定理，你能发现AP²+CP²与BP²+DP²的数量关系为

  ．
  
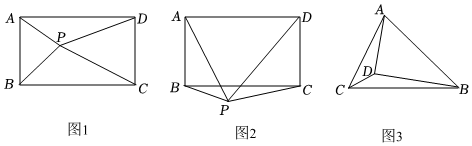
  探究：如图2，P是矩形ABCD外任意一点，上面的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由．
  应用：如图3，在△ABC中，CA=6，CB=8，D是△ABC内一点，且CD=2，∠ADB=90°，求AB的最小值．
  组卷：498引用：3难度：0.2

  解析