2022-2023学年重庆十八中高二（下）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分，在每个小题给出的选项中，只有一项是符合题目要求的.

• 1．已知函数f（x）=cosx,则f′（

  π

  3

  ）等于（　　）

  A． 1 2

  B．- 1 2

  C．- 3 2

  D． 3 2
  组卷：193引用：5难度：0.9

  解析

• 2．用数字1，2，3，4组成没有重复数字的四位数，其中奇数和偶数互不相邻的个数为（　　）

  A．6

  B．8

  C．12

  D．24
  组卷：94引用：2难度：0.7

  解析

• 3．若函数f（x）=x+alnx在区间（1，2）内存在单调递减区间，则实数a的取值范围是（　　）

  A．（-∞，-1）

  B．（-∞，-1]

  C．（-∞，-2）

  D．（-∞，-2]
  组卷：231引用：3难度：0.6

  解析

• 4．曲线

  y

  =

  4

  e

  x

  +

  1

  在点P（0，2）处的切线的斜率为（　　）

  A．-1

  B．1

  C．-4

  D．4
  组卷：66引用：3难度：0.7

  解析

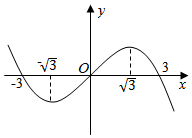• 5．设三次函数f（x）的导函数为f′（x），函数y=x•f′（x）的图象的一部分如图所示，则正确的是（　　）

  A．f（x）的极大值为 f （ 3 ） ，极小值为 f （ - 3 ）

  B．f（x）的极大值为 f （ - 3 ） ，极小值为 f （ 3 ）

  C．f（x）的极大值为f（-3），极小值为f（3）

  D．f（x）的极大值为f（3），极小值为f（-3）
  组卷：3345引用：40难度：0.7

  解析

• 6．设球的半径为时间t的函数R（t）．若球的体积以均匀速度c增长，则球的表面积的增长速度与球半径．

  A．成正比，比例系数为C	B．成正比，比例系数为2C
  C．成反比，比例系数为C	D．成反比，比例系数为2C
  组卷：549引用：14难度：0.9

  解析

• 7．用a代表红球，b代表蓝球，c代表黑球，由加法原理及乘法原理，从1个红球和1个蓝球中取出若干个球的所有取法可由（1+a）（1+b）的展开式1+a+b+ab表示出来，如：“1”表示一个球都不取、“a”表示取出一个红球，而“ab”则表示把红球和蓝球都取出来．以此类推，下列各式中，其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球，且所有的蓝球都取出或都不取出的所有取法的是（　　）

  A．（1+a+a2+a3+a4+a5）（1+b5）（1+c）5

  B．（1+a5）（1+b+b2+b3+b4+b5）（1+c）5

  C．（1+a）5（1+b+b2+b3+b4+b5）（1+c5）

  D．（1+a5）（1+b）5（1+c+c2+c3+c4+c5）
  组卷：835引用：9难度：0.7

  解析

四、解答题：本题共6小题，共70分

• 21．已知函数f（x）=e^x+ax-1，x∈R．
  （1）若f（x）≥0恒成立，求实数a的取值集合；
  （2）设m为整数，若对任意正整数n都有

  （

  1

  +

  1

  3

  ）

  （

  1

  +

  1

  3

  2

  ）

  ⋯

  （

  1

  +

  1

  3

  n

  ）

  ＜

  m

  ，求m的最小值．
  组卷：65引用：3难度：0.3

  解析

• 22．已知函数
  f（x）=（cosx-x）（π+2x）-

  8

  3

  （sinx+1）
  g（x）=3（x-π）cosx-4（1+sinx）ln（3-

  2

  x

  π

  ）
  证明：
  （Ⅰ）存在唯一x₀∈（0，

  π

  2

  ），使f（x₀）=0；
  （Ⅱ）存在唯一x₁∈（

  π

  2

  ，π），使g（x₁）=0，且对（Ⅰ）中的x₀，有x₀+x₁＜π．
  组卷：2084引用：12难度：0.1

  解析