2022-2023学年重庆八中九年级（下）定时练习数学试卷（4月份）

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

• 1．多项式x²-2x-3的一次项系数是（　　）

  A．-2x

  B．-2

  C．2x

  D．2
  组卷：768引用：3难度：0.7

  解析

• 2．下列图形中，属于轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：99引用：2难度：0.9

  解析

• 3．若二次根式

  2

  -

  x

  在实数范围内有意义，则下列各数中，x可取的值是（　　）

  A．4

  B．π

  C．-1

  D．3
  组卷：135引用：3难度：0.7

  解析

• 4．要在墙上钉牢一根木条，至少要钉两颗钉子．能正确解释这一现象的数学知识是（　　）

  A．两点之间，线段最短

  B．垂线段最短

  C．两点确定一条直线

  D．经过一点有且只有一条直线与已知直线垂直
  组卷：804引用：7难度：0.9

  解析

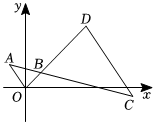• 5．如图，△AOB与△CDB关于点B位似，其中B（1，1），D（4，4），则△AOB与△CDB的面积之比是（　　）

  A．1：4

  B．1：3

  C．1：16

  D．1：9
  组卷：491引用：4难度：0.7

  解析

• 6．已知关于x、y的二元一次方程mx-n=y,下表列出了当x分别取值时对应的y值．则关于x的不等式mx-n≤2的解集为（　　）
  

  x	…	-2	-1	0	1	2	3	…
  y	…	3	2	1	0	-1	-2	…

  A．x＜-1

  B．x≤-1

  C．x≥-1

  D．x＞-1
  组卷：284引用：2难度：0.7

  解析

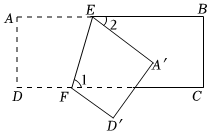• 7．如图，四边形ABCD为一矩形纸带，点E、F分别在边AB、CD上，将纸带沿EF折叠，点A、D的对应点分别为A'、D'，若∠2=α，则∠1的度数为（　　）

  A．2α

  B．90°-α

  C． 90 ° - 1 3 α

  D． 90 ° - 1 2 α
  组卷：1649引用：7难度：0.6

  解析

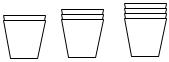• 8．如图，两个相同的某种杯子叠放在一起的高度为13cm,三个该种杯子叠放的高度是16cm,四个该种杯子叠放的高度是19cm,那么8个该种杯子叠放在一起高度为（　　）

  A．31cm

  B．28cm

  C．34cm

  D．24cm
  组卷：101引用：2难度：0.7

  解析

三、解答题：（本大题共8个小题，19题8分，20-26每小题8分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

• 25．如图，在平面直角坐标系中，抛物线y=-x²+bx+c经过A（0，1），B（4，-1）．直线AB交x轴于点C，P是直线AB上方且在对称轴右侧的一个动点，过P作PD⊥AB，垂足为D，E为点P关于抛物线的对称轴的对应点．
  （1）求抛物线的函数表达式；
  （2）当

  5

  PD

  +

  PE

  的最大值时，求此时点P的坐标和

  5

  PD

  +

  PE

  的最大值；
  （3）将抛物线y关于直线x=3作对称后得新抛物线y'，新抛物线与原抛物线相交于点F，M是新抛物线对称轴上一点，N是平面中任意一点，是否存在点N，使得以C，F，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．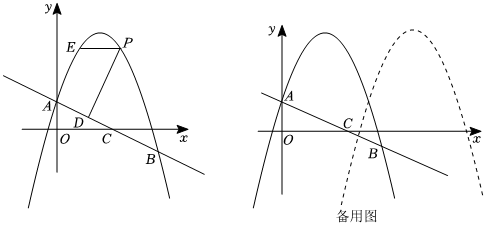
  
  组卷：452引用：2难度：0.1

  解析

• 26．△ABC中，∠B=60°．
  
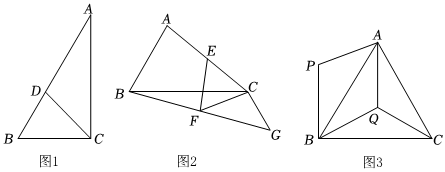
  （1）如图1，若AC＞BC，CD平分∠ACB交AB于点D，且AD=

  3

  BD．证明：∠A=30°；
  （2）如图2，若AC＜BC，取AC中点E，将CE绕点C逆时针旋转60°至CF，连接BF并延长至G，使BF=FG，猜想线段AB、BC、CG之间存在的数量关系，并证明你的猜想；
  （3）如图3，若AC=BC，P为平面内一点，将△ABP沿直线AB翻折至△ABQ，当3AQ+2BQ+

  13

  CQ取得最小值时，直接写出

  BP

  CQ

  的值．
  组卷：376引用：2难度：0.1

  解析