2022-2023学年山东省枣庄市高一（下）质检数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知向量

  a

  =

  （

  1

  ，

  λ

  ）

  ，

  b

  =

  （

  μ

  ，

  2

  ）

  ，若

  a

  ∥

  b

  ，则（　　）

  A．μ=2λ

  B．μ=-2λ

  C．λμ=2

  D．λμ=-2
  组卷：82引用：3难度：0.8

  解析

• 2．已知复数z满足z-

  z

  =0，且z•

  z

  =4，则z=（　　）

  A．2

  B．2i

  C．±2

  D．±2i
  组卷：277引用：5难度：0.9

  解析

• 3．一个圆台的上、下底面的半径分别为1，4，母线长为5，则该圆台的侧面积为（　　）

  A．30π

  B．25π

  C．20π

  D．15π
  组卷：115引用：2难度：0.7

  解析

• 4．将一枚质地均匀的骰子连续抛掷2次，至少出现一次6点的概率为（　　）

  A． 13 18

  B． 25 36

  C． 11 36

  D． 5 18
  组卷：145引用：2难度：0.8

  解析

• 5．一组数据x₁，x₂，…，x₂₀₂₃（x₁＜x₂＜…＜x₂₀₂₃），记其均值为

  x

  ，第25百分位数为m,方差为s²，则（　　）

  A．m=x505

  B． x 1012 ＜ x ＜ x 1013

  C．数据ax1+b,ax2+b,…，ax2023+b的均值为 a x

  D．数据ax1+b,ax2+b,…，ax2023+b的方差为a2s2
  组卷：99引用：3难度：0.7

  解析

• 6．已知i为虚数单位，若实数a使得ai+a²（i²⁰²³+1）-1为纯虚数，则a=（　　）

  A．-1

  B．1

  C．±1

  D．2
  组卷：68引用：2难度：0.7

  解析

• 7．某班50名学生骑自行车，骑电动车到校所需时间统计如表：
  

  到校方式	人数	平均用时（分钟）	方差
  骑自行车	20	30	36
  骑电动车	30	20	16

  则这50名学生到校时间的方差为（　　）

  A．48

  B．46

  C．28

  D．24
  组卷：85引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

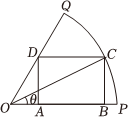• 21．如图，在扇形OPQ中，半径OQ=1，圆心角

  ∠

  POQ

  =

  π

  3

  ，C是扇形弧上的动点，矩形ABCD内接于扇形，设∠POC=θ．
  （1）试建立矩形ABCD的面积S关于θ的函数关系式；
  （2）在（1）的条件下，当θ为何值时，S取最大值，并求出最大值．
  组卷：172引用：3难度：0.6

  解析

• 22．△ABC的内角A，B，C的对边分别为a,b,c,且

  acos

  C

  +

  1

  2

  c

  =

  b

  ．
  （1）求A；
  （2）已知b＜c,∠BAC的平分线交BC于点D，

  AD

  =

  4

  3

  3

  ，边BC上的中线

  AE

  =

  7

  ，求a,b,c.
  组卷：153引用：2难度：0.4

  解析