2022-2023学年安徽省六安市金安区田家炳实验中学高一（下）期末数学试卷

一、单选题（共8小题，每题5分，满分40分）

• 1．设复数z=

  3

  -

  i

  1

  +

  i

  ，则复数z的虚部为（　　）

  A．-2i

  B．-2

  C．2i

  D．2
  组卷：61引用：6难度：0.9

  解析

• 2．某高中共有学生1200人，其中高一、高二、高三的学生人数比为6：5：4，现用分层抽样的方法从该校所有学生中抽取一个容量为60的样本，则高三年级应该抽取（　　）人．

  A．16

  B．18

  C．20

  D．24
  组卷：375引用：8难度：0.8

  解析

• 3．下列说法正确的是（　　）

  A．若直线l平行于平面α内的无数条直线，则l∥α

  B．若直线a在平面α外，则a∥α

  C．若直线a∥b,b⊂α，则a∥α

  D．若直线a∥b,b⊂α，则直线a就平行于平面内的无数条直线
  组卷：319引用：10难度：0.9

  解析

• 4．直线l⊥平面α，直线m⊂α，则l与m不可能（　　）

  A．平行

  B．相交

  C．异面

  D．垂直
  组卷：104引用：3难度：0.8

  解析

• 5．已知圆锥的底面半径为1，其侧面展开图是一个圆心角为120°的扇形，则此圆锥的母线长为（　　）

  A．2

  B．3

  C．4

  D．6
  组卷：111引用：6难度：0.8

  解析

• 6．已知正四棱锥S-ABCD的底面边长为2，侧棱长为

  3

  ，则该正四棱锥的体积等于（　　）

  A． 4 3

  B． 4 3 3

  C．4 3

  D．4
  组卷：214引用：3难度：0.7

  解析

• 7．已知三棱锥A-BCD的所有顶点都在球O的球面上，且AB⊥平面BCD，AB=2

  3

  ，AC=AD=4，CD=2

  2

  ，则球O的表面积为（　　）

  A．20π

  B．18π

  C．36π

  D．24π
  组卷：660引用：10难度：0.5

  解析

四、解答题（共6小题，其中第17题10分，其余各题12分，满分70分）

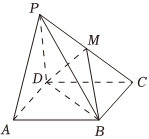• 21．如图，在四棱锥D-ABCD中，底面四边形ABCD是菱形，M为PC的中点．
  （1）求证：PA∥平面BDM；
  （2）若PA=PC，求证：平面PBD⊥平面ABCD．
  组卷：303引用：2难度：0.5

  解析

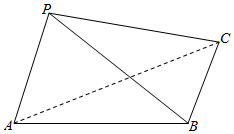• 22．如图，在三棱锥P-ABC中，AP⊥PC，AB⊥BC，AC=2，∠ACP=30°，AB=BC．
  （1）当PB=

  2

  时，求证：平面ABC⊥平面PAC；
  （2）当AP⊥BC时，求三棱锥A-PBC的体积．
  组卷：108引用：2难度：0.5

  解析