2022-2023学年山东省泰安市新泰一中老校区高一（下）第二次段考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每个小题绐岀的四个选项中，只有一项是符合题目要求的.

• 1．若复数

  3

  i

  1

  +

  2

  i

  （

  1

  -

  a

  3

  i

  ）

  （a∈R，i为虚数单位）是纯虚数，则实数a的值为（　　）

  A．-2

  B．6

  C．4

  D．-6
  组卷：57引用：5难度：0.8

  解析

• 2．在△ABC中，若∠A=60°，b=1，

  S

  △

  ABC

  =

  3

  ，则

  a

  +

  b

  +

  c

  sin

  A

  +

  sin

  B

  +

  sin

  C

  的值为（　　）

  A． 26 3 3

  B． 2 39 3

  C． 39 3

  D． 13 3 3
  组卷：63引用：2难度：0.7

  解析

• 3．已知口袋内有一些大小相同的红球、白球和黄球，从中任意摸出一球，摸出的球是红球或白球的概率为0.4，摸出的球是红球或黄球的概率为0.9，则摸出的球是黄球或白球的概率为（　　）

  A．0.7

  B．0.5

  C．0.3

  D．0.6
  组卷：165引用：3难度：0.7

  解析

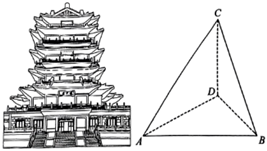• 4．“近水亭台草木欣，朱楼百尺回波濆”，位于济南大明湖畔的超然楼始建于元代，历代因战火及灾涝等原因，屡毁屡建．今天我们所看到的超然楼为2008年重建而成，共有七层，站在楼上观光，可俯视整个大明湖的风景．如图，为测量超然楼的高度，小刘取了从西到东相距104（单位：米）的A，B两个观测点，在A点测得超然楼在北偏东60°的点D处（A，B，D在同一水平面上），在B点测得超然楼在北偏西30°，楼顶C的仰角为45°，则超然楼的高度CD（单位：米）为（　　）

  A．26

  B． 26 3

  C．52

  D． 52 3
  组卷：132引用：4难度：0.7

  解析

• 5．设m,n,l分别是三条不同的直线，α是平面，则下列结论中正确的是（　　）

  A．若m⊥n,m⊥l,n⊂α，l⊂α，则m⊥α

  B．若m⊥n,n⊂α，则m⊥α

  C．若m∥n,n⊥α，则m⊥α

  D．若m∥α，n⊂α，则m∥n
  组卷：23引用：3难度：0.6

  解析

• 6．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ）

  ，

  c

  =

  （

  4

  ，

  5

  ）

  ．若

  a

  与

  b

  +

  λ

  c

  垂直，则实数λ的值为（　　）

  A． 1 14

  B． - 4 7

  C．3

  D． 4 11
  组卷：214引用：6难度：0.7

  解析

• 7．如图，在四棱锥S-ABCD中，SA⊥平面ABCD，四边形ABCD为平行四边形，∠ABC=60°且SA=AB=BC=2，E为SA的中点，则异面直线SC与DE所成的角的余弦值为（　　）

  A． 2 5 5

  B． 10 5

  C． 5 5

  D． 15 5
  组卷：568引用：6难度：0.5

  解析

四．解答题：本题共6小题，17题10分，剩下每题12分。共70分，解答应写出文字说明、证明过程或演算步骤

• 21．（1）抛掷两枚质地均匀的骰子，设A=“第一次出现奇数点”，B=“两枚骰子点数之和为3的倍数”，判断事件A与事件B是否相互独立，并说明理由；
  （2）甲乙两名射击运动员进行射击考核测试，每人每次有两次射击机会，若两次机会中至少有一次中靶，则考核通过．已知甲的中靶概率是0.7，乙的中靶概率是0.6，甲乙两人射击互不影响．求两人中恰有一人通过考核的概率．
  组卷：31引用：2难度：0.7

  解析

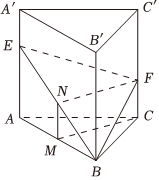• 22．如图，在正三棱柱ABC-A'B'C'中，E为AA'上的点，F为CC'上的点，M，N分别为BA，BE的中点，CM∥平面BEF．
  （1）证明：M，N，F，C四点共面，且平面BEF⊥平面ABB'A'；
  （2）若AB=2，AE=4，求平面BEF与平面AA'C'C所成锐二面角的余弦值．
  组卷：44引用：2难度：0.6

  解析