2022-2023学年北京市海淀区首都师大二附中九年级（上）期中数学试卷

一、选择题（本大题共8小题，共24分）

• 1．“瓦当”是中国古建筑中覆盖檐头筒瓦前端的遮挡，主要有防水、排水、保护木制飞檐和美化屋面轮廓的作用．瓦当上的图案设计优美，字体行云流水，极富变化，是中国特有的文化艺术遗产．下面“瓦当”图案中既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：431引用：25难度：0.9

  解析

• 2．边长为2的正方形内接于⊙O，则⊙O的半径是（　　）

  A．1

  B． 2

  C．2

  D．2 2
  组卷：484引用：6难度：0.5

  解析

• 3．抛物线y=-x²+2和y=-（x+2）²的对称轴分别是（　　）

  A．y轴，直线x=2	B．直线x=2，x=-2
  C．直线x=-2，直线x=2	D．y轴，直线x=-2
  组卷：497引用：4难度：0.6

  解析

• 4．已知m是关于x的方程x²-2x-3=0的一个根，则2m²-4m+2=（　　）

  A．5

  B．8

  C．-8

  D．6
  组卷：906引用：14难度：0.6

  解析

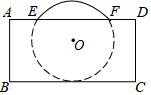• 5．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4cm,则球的半径长是（　　）

  A．2cm

  B．2.5cm

  C．3cm

  D．4cm
  组卷：5039引用：41难度：0.9

  解析

• 6．如图，四边形ABCD内接于⊙O，∠D=110°，则∠AOC的度数是（　　）

  A．55°

  B．110°

  C．130°

  D．140°
  组卷：791引用：8难度：0.7

  解析

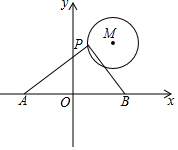• 7．如图，⊙M的半径为2，圆心M的坐标为（3，4），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：3460引用：18难度：0.5

  解析

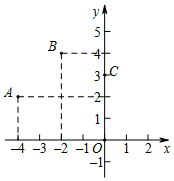• 8．如图，二次函数y=ax²+bx+c（a≠0）的图象经过点A，B，C．现有下面四个推断：
  ①抛物线开口向下；
  ②当x=-2时，y取最大值；
  ③当m＜4时，关于x的一元二次方程ax²+bx+c=m必有两个不相等的实数根；
  ④直线y=kx+c（k≠0）经过点A，C，当kx+c＞ax²+bx+c时，x的取值范围是-4＜x＜0；
  其中推断正确的是（　　）

  A．①②

  B．①③

  C．①③④

  D．②③④
  组卷：1797引用：20难度：0.5

  解析

三、解答题（本大题共52分，第17-20题，每小题4分，第21-22题，每小题4分，第23-24题，每小题4分，第25-26题，每小题4分）

• 25．已知正方形ABCD，将线段BA绕点B旋转α（0°＜α＜90°），得到线段BE，连接EA，EC．
  （1）如图1，当点E在正方形ABCD的内部时，若BE平分∠ABC，AB=4，则∠AEC=

  °，四边形ABCE的面积为

  ；
  （2）当点E在正方形ABCD的外部时，
  ①在图2中依题意补全图形，并求∠AEC的度数；
  ②作∠EBC的平分线BF交EC于点G，交EA的延长线于点F，连接CF．用等式表示线段AE，FB，FC之间的数量关系，并证明．
  
  组卷：2296引用：11难度：0.4

  解析

• 26．如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为H，且交⊙I于P，Q两点（Q在P，H之间）我们把点P称为⊙I关于直线a的“远点”，把PQ•PH的值称为⊙I关于直线a的“特征数”．
  （1）如图2，在平面直角坐标系xOy中，点E的坐标为（0，4），半径为1的⊙O与两坐标轴交于点A，B，C，D．
  ①过点E作垂直于y轴的直线m,则⊙O关于直线m的“远点”是点

  （填“A”，“B”，“C”或“D”），⊙O关于直线m的“特征数”为

  ；
  ②若直线n的函数表达式为y=

  3

  x+4，求⊙O关于直线n的“特征数”；
  （2）在平面直角坐标系xOy中，直线l经过点M（1，4），点F是坐标平面内一点，以F为圆心，

  3

  为半径作⊙F．若⊙F与直线l相离，点N（-1，0）是⊙F关于直线l的“远点”，且⊙F关于直线l的“特征数”是6

  6

  ，直接写出直线l的函数解析式．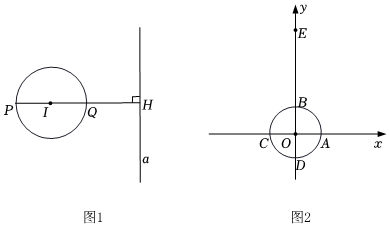
  
  组卷：665引用：3难度：0.1

  解析