当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省金华市十校高一（下）期末数学试卷

发布：2024/7/6 8:0:9

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合
A
=
{
x
|
-
1
≤
x
≤
1
}
，
B
=
{
x
|
x
x
-
2
≤
0
}
，则A∩B=（　　）
A．{x|-1≤x≤2} B．{x|-1≤x＜2} C．{x|0≤x≤1} D．{x|0≤x≤2}
组卷：682引用：3难度：0.8
解析
2．已知i是虚数单位，复数z₁=4+2i与z₂=3+ai的模相等，则实数a的值为（　　）
A．
±
11
B．
11
C．±11 D．11
组卷：47引用：2难度：0.7
解析
3．设函数
f
（
x
）
=
（
1
2
）
x
2
-
2
mx
在区间（1，2）上单调递增，则m的取值范围为（　　）
A．（-∞，-2] B．[-2，-1] C．[1，2] D．[2，+∞）
组卷：223引用：3难度：0.6
解析
4．已知△ABC的内角A，B，C的对边分别是a,b,c,面积S满足a²-4S=c²+b²，则A=（　　）
A．
π
4
B．
π
3
C．
2
π
3
D．
3
π
4
组卷：143引用：2难度：0.7
解析
5．已知向量
a
=
（
1
，
2
）
，
b
=
（
-
3
，
1
）
，则向量
a
在向量
b
方向上的投影向量是（　　）
A．
-
b
10
B．
b
10
C．
-
10
10
b
D．
10
10
b
组卷：127引用：4难度：0.8
解析
6．已知α，β，γ表示三个不同平面，a,b,c表示三条不同直线，则使“a∥b∥c”成立的一个充分非必要条件是（　　）
A．若a⊥α，b⊥β，c⊥γ，且α⊥β，β⊥γ，γ⊥α
B．若a∥α，b∥β，c∥γ，且α∥β∥γ
C．若α∩β=a,β∩γ=b,γ∩α=c
D．若α∩β=a,b⊂α，c⊂β，b∥c
组卷：90引用：2难度：0.7
解析
7．一个圆柱形粮仓，高1丈3尺
3
1
3
寸，可容纳米2000斛，已知1丈=10尺=100寸，1斛米=1620立方寸，若π取3，则该圆柱形粮仓底面的周长是（　　）
A．440寸 B．540寸 C．560寸 D．640寸
组卷：40引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

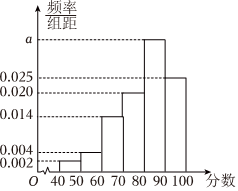21．树人中学2000名师生参加了对学校教学管理满意度的评分调查，按样本量比例分配的分层随机抽样方法，抽取100个师生的评分（满分100分），绘制如图所示的频率分布直方图，并将分数从低到高分为四个等级：

满意度评分低于60分 60分到79分 80分到89分 90分及以上

满意度等级不满意基本满意满意非常满意

（1）求图中a的值；
（2）若师生的满意指数不低于0.8，则该校可获评“教学管理先进单位”，根据你所学的统计知识，判断该校是否能获奖，并说明理由．（注：满意指数=
满意度的平均数
100
）
（3）假设在样本中，学生、教师的人数分别为m、n（1≤n＜m＜100，m,n∈N）．记所有学生的评分为x₁、x₂、⋯、x_m，其平均数为
x
，方差为
s
2
x
，所有教师的评分为y₁、y₂、⋯、y_n，其平均数为
y
，方差为
s
2
y
，总样本评分的平均数为
z
，方差为s²，若
x
=
y
，
s
2
=
4
5
s
x
•
s
y
，试估计该校等级为满意的学生的最少人数．

组卷：117引用：2难度：0.5

解析

22．已知函数f（x）=ax³+bx+1．
（1）若f（log₂x）=2023，求f（log_0.5x）的值；
（2）已知函数f（x）的图象经过（1，-1），（2，3），
（ⅰ）若f（t）=0，求
f
（
1
-
1
t
）
的值；
（ⅱ）若f（x）的三个零点为x₁，x₂，x₃，且x₁＜x₂＜x₃，求
（
x
2
1
-
x
2
-
2
）
（
x
2
2
-
x
3
-
2
）
（
x
2
3
-
x
1
-
2
）
的值．
组卷：97引用：2难度：0.5
解析