当前位置：试卷中心 > 试卷详情

2021-2022学年吉林省长春市清蒲中学高二（上）月考数学试卷（12月份）

发布：2025/11/1 4:0:25

一、单选题（60分）

1．若直线l₁：（m+1）x+6y+4=0与l₂：x+3my+1=0平行，则m的值为（　　）
A．-2 B．-1或-2 C．1或-2 D．1
组卷：98引用：3难度：0.8
2．已知向量
a
=
（
0
，-
1
，
1
）
与
b
=
（
0
，
2
k
-
3
，
k
2
）
共线，则实数k=（　　）
A．0 B．1 C．-1或3 D．-3或1
组卷：53引用：1难度：0.7
3．抛物线y=4x²的准线方程为（　　）
A．x=-1 B．y=-1 C．x=-
1
16
D．y=-
1
16
组卷：1082引用：24难度：0.9
4．已知F₁（-8，3），F₂（2，3），动点P满足|PF₁|-|PF₂|=10，则P点轨迹是（　　）
A．双曲线 B．双曲线一支 C．直线 D．一条射线
组卷：86引用：2难度：0.7
5．直线l经过A（-2，3），B（-1，2）两点，则直线l的倾斜角是（　　）
A．
π
4
B．
3
π
4
C．
π
3
D．
2
π
3
组卷：331引用：4难度：0.8
6．在平面直角坐标系中，已知点A（-1，0），B（2，0），圆
C
：
（
x
-
2
）
2
+
（
y
-
m
）
2
=
1
4
（
m
＞
0
）
，在圆上存在点P满足|PA|=2|PB|，则实数m的取值范围是（　　）
A．
[
2
2
，
6
2
]
B．
[
5
4
，
21
2
]
C．
（
0
，
21
2
]
D．
[
5
2
，
21
2
]
组卷：426引用：11难度：0.5
7．已知M是圆C：x²+y²=1上一个动点，且直线l₁：mx-ny-3m+n=0与直线l₂：nx+my-3m-n=0（m,n∈R，m²+n²≠0）相交于点P，则|PM|的取值范围是（　　）
A．
[
3
-
1
，
2
3
+
1
]
B．
[
2
-
1
，
2
2
+
1
]
C．
[
2
-
1
，
3
2
+
1
]
D．
[
2
-
1
，
3
3
+
1
]
组卷：585引用：17难度：0.6
8．双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦点分别为F₁，F₂，过F₁的直线与双曲线C的右支在第一象限的交点为A，与y轴的交点为B，且B为AF₁的中点，若△ABF₂的周长为6a,则双曲线C的渐近线方程为（　　）
A．
y
=±
3
x
B．
y
=±
2
x
C．
y
=±
3
2
x
D．
y
=±
2
2
x
组卷：703引用：6难度：0.5
9．从1到10的连续10个整数中随机抽取3个，已知这3个数之和为奇数，则这3个数之积为偶数的概率为（　　）
A．
5
12
B．
5
6
C．
1
12
D．
2
3
组卷：37引用：2难度：0.7
10．圆（x+4）²+（y-3）²=7的圆心和半径分别是（　　）
A．（-4，3），7 B．
（
-
4
，
3
）
，
7
C．（4，-3），7 D．
（
4
，-
3
）
，
7
组卷：234引用：2难度：0.9
11．已知空间向量
a
=
（
2
，
0
，
1
）
，
b
=
（
-
1
，
2
，
1
）
，
c
=
（
0
，
4
，
z
）
，若向量
a
，
b
，
c
共面，则实数z=（　　）
A．1 B．2 C．3 D．4
组卷：170引用：7难度：0.5
12．抛物线y²=2px过点
（
1
，
3
）
，求焦点（　　）
A．（
3
12
，0） B．（
3
6
，0） C．
（
3
4
，
0
）
D．
（
3
2
，
0
）
组卷：1448引用：2难度：0.8

二、填空题（20分）

13．设直线3x+4y-5=0与圆C₁：x²+y²=4交于A，B两点，若圆C₂的圆心在线段AB上，且圆C₂与圆C₁相切，切点在圆C₁的劣弧
ˆ
AB
上，则圆C₂的半径的最大值是
．
组卷：347引用：13难度：0.5
14．已知双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的渐近线方程为y=±2x,则C的离心率为
．
组卷：148引用：4难度：0.7
15．已知椭圆中心在原点，一个焦点为F（-2
3
，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是
．
组卷：891引用：21难度：0.7
16．在平面斜坐标系xOy中，∠xOy=60°，平面上任一点P关于斜坐标系的斜坐标是这样定义的：若
OP
=
x
e
1
+
y
e
2
（其中
e
1
，
e
2
分别为x,y轴方向相同的单位向量），则P的坐标为（x,y），若P关于斜坐标系xOy的坐标为（2，-1），则
|
OP
|
=
组卷：242引用：7难度：0.7

三、解答题（70分）

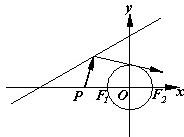17．已知圆O：x²+y²=1，直线l：
y
=
3
3
（
x
+
4
）
．
（1）设圆O与x轴的两交点是F₁，F₂，若从F₁发出的光线经l上的点M反射后过点F₂，求以F₁，F₂为焦点且经过点M的椭圆方程；
（2）点P是x轴负半轴上一点，从点P发出的光线经l反射后与圆O相切．若光线从射出经反射到相切经过的路程最短，求点P的坐标．
组卷：32引用：2难度：0.5
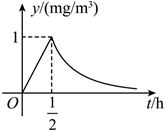18．流感是由流感病毒引起的一种急性呼吸道传染病，冬天空气干燥、寒冷，大多数人喜欢待在较为密闭的空间里，而这样的空间空气流通性不强，有利于流感病毒的传播．为了预防流感，某学校决定对教室用药熏消毒法进行消毒，已知药物释放过程中，室内每立方米空气中的含药量y（单位：毫克）与时间t（单位：小时）成正比例；药物释放完毕后，y与t的函数关系式为
y
=
（
1
32
）
t
+
a
（a为常数），如图所示
（1）求从药物释放开始，室内每立方米空气中的含药量y（单位：毫克）与时间t（单位：小时）的函数关系式；
（2）实验表明，当室内每立方米空气中药物含量不超过0.125毫克时对人体无害，求从药物释放开始，同学们至少要经过多少分钟方可进入教室．
组卷：16引用：3难度：0.6
19．已知抛物线C：y²=2px（p＞0）的焦点为F，点P（x₀，p）在抛物线C上，Q（-1，0），|FP|=|FQ|+1．
（1）求C的方程；
（2）过F的直线l与C相交于A，B两点，若AB的垂直平分线与C相交于M，N两点，且A，M，B，N四点在同一个圆上，求l的方程．
组卷：20引用：3难度：0.5
20．已知椭圆的焦点坐标为F₁（-1，0），F₂（1，0），且短轴的一个端点B满足
B
F
1
•
B
F
2
=2．
（1）求椭圆的方程；
（2）如果过F₂的直线与椭圆交于不同的两点M，N，那么△F₁MN的内切圆半径是否存在最大值？若存在，求出最大值及此时直线的方程，若不存在，说明理由．
组卷：54引用：1难度：0.3
21．已知椭圆
Γ
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
左右焦点分别为F₁、F₂，离心率为
3
2
．斜率为k（k＞0）的直线l（不过原点）交椭圆于两点A、B，当直线l过F₁时，△AF₂B周长为8．
（1）求椭圆Γ的方程；
（2）设OA、OB斜率分别为k₁、k₂，且k₁、k、k₂依次成等比数列，求k的值，并求当△AOB面积为
7
4
时，直线l的方程．
组卷：22引用：2难度：0.5
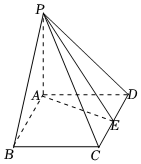22．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为菱形，∠ABC=60°，AP=AB，E为CD的中点．
（1）求证：CD⊥平面PAE；
（2）求平面PAE与平面PBC所成二面角的正弦值．
组卷：751引用：21难度：0.5

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2021-2022学年吉林省长春市清蒲中学高二（上）月考数学试卷（12月份）

一、单选题（60分）

1．若直线l1：（m+1）x+6y+4=0与l2：x+3my+1=0平行，则m的值为（ ）

2．已知向量a=（0，-1，1）与b=（0，2k-3，k2）共线，则实数k=（ ）

3．抛物线y=4x2的准线方程为（ ）

4．已知F1（-8，3），F2（2，3），动点P满足|PF1|-|PF2|=10，则P点轨迹是（ ）

5．直线l经过A（-2，3），B（-1，2）两点，则直线l的倾斜角是（ ）

6．在平面直角坐标系中，已知点A（-1，0），B（2，0），圆C：（x-2）2+（y-m）2=14（m＞0），在圆上存在点P满足|PA|=2|PB|，则实数m的取值范围是（ ）

7．已知M是圆C：x2+y2=1上一个动点，且直线l1：mx-ny-3m+n=0与直线l2：nx+my-3m-n=0（m,n∈R，m2+n2≠0）相交于点P，则|PM|的取值范围是（ ）

8．双曲线C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦点分别为F1，F2，过F1的直线与双曲线C的右支在第一象限的交点为A，与y轴的交点为B，且B为AF1的中点，若△ABF2的周长为6a,则双曲线C的渐近线方程为（ ）

9．从1到10的连续10个整数中随机抽取3个，已知这3个数之和为奇数，则这3个数之积为偶数的概率为（ ）

10．圆（x+4）2+（y-3）2=7的圆心和半径分别是（ ）

11．已知空间向量a=（2，0，1），b=（-1，2，1），c=（0，4，z），若向量a，b，c共面，则实数z=（ ）

12．抛物线y2=2px过点（1，3），求焦点（ ）

二、填空题（20分）

13．设直线3x+4y-5=0与圆C1：x2+y2=4交于A，B两点，若圆C2的圆心在线段AB上，且圆C2与圆C1相切，切点在圆C1的劣弧ˆAB上，则圆C2的半径的最大值是．

14．已知双曲线C：x2a2-y2b2=1（a＞0，b＞0）的渐近线方程为y=±2x,则C的离心率为 ．

15．已知椭圆中心在原点，一个焦点为F（-23，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 ．

16．在平面斜坐标系xOy中，∠xOy=60°，平面上任一点P关于斜坐标系的斜坐标是这样定义的：若OP=xe1+ye2（其中e1，e2分别为x,y轴方向相同的单位向量），则P的坐标为（x,y），若P关于斜坐标系xOy的坐标为（2，-1），则|OP|=

三、解答题（70分）

22．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为菱形，∠ABC=60°，AP=AB，E为CD的中点．（1）求证：CD⊥平面PAE；（2）求平面PAE与平面PBC所成二面角的正弦值．

1．若直线l₁：（m+1）x+6y+4=0与l₂：x+3my+1=0平行，则m的值为（　　）

2．已知向量
a
=
（
0
，-
1
，
1
）
与
b
=
（
0
，
2
k
-
3
，
k
2
）
共线，则实数k=（　　）

3．抛物线y=4x²的准线方程为（　　）

4．已知F₁（-8，3），F₂（2，3），动点P满足|PF₁|-|PF₂|=10，则P点轨迹是（　　）

5．直线l经过A（-2，3），B（-1，2）两点，则直线l的倾斜角是（　　）

6．在平面直角坐标系中，已知点A（-1，0），B（2，0），圆
C
：
（
x
-
2
）
2
+
（
y
-
m
）
2
=
1
4
（
m
＞
0
）
，在圆上存在点P满足|PA|=2|PB|，则实数m的取值范围是（　　）

7．已知M是圆C：x²+y²=1上一个动点，且直线l₁：mx-ny-3m+n=0与直线l₂：nx+my-3m-n=0（m,n∈R，m²+n²≠0）相交于点P，则|PM|的取值范围是（　　）

8．双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦点分别为F₁，F₂，过F₁的直线与双曲线C的右支在第一象限的交点为A，与y轴的交点为B，且B为AF₁的中点，若△ABF₂的周长为6a,则双曲线C的渐近线方程为（　　）

9．从1到10的连续10个整数中随机抽取3个，已知这3个数之和为奇数，则这3个数之积为偶数的概率为（　　）

10．圆（x+4）²+（y-3）²=7的圆心和半径分别是（　　）

11．已知空间向量
a
=
（
2
，
0
，
1
）
，
b
=
（
-
1
，
2
，
1
）
，
c
=
（
0
，
4
，
z
）
，若向量
a
，
b
，
c
共面，则实数z=（　　）

12．抛物线y²=2px过点
（
1
，
3
）
，求焦点（　　）

13．设直线3x+4y-5=0与圆C₁：x²+y²=4交于A，B两点，若圆C₂的圆心在线段AB上，且圆C₂与圆C₁相切，切点在圆C₁的劣弧
ˆ
AB
上，则圆C₂的半径的最大值是
．

14．已知双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的渐近线方程为y=±2x,则C的离心率为
．

15．已知椭圆中心在原点，一个焦点为F（-2
3
，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是
．

22．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为菱形，∠ABC=60°，AP=AB，E为CD的中点．
（1）求证：CD⊥平面PAE；
（2）求平面PAE与平面PBC所成二面角的正弦值．