2023年吉林省长春外国语学校中考数学质检试卷（二）

一、选择题（每小题3分，共24分）

• 1．1与-2023的差是（　　）

  A．-2024

  B．2024

  C．-2022

  D．2022
  组卷：645引用：3难度：0.9

  解析

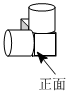• 2．我国古代数学家利用“牟合方盖”找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图所示的几何体是可以形成“牟合方盖”的一种模型，它从正面看是（　　）

  A．

  B．

  C．

  D．
  组卷：175引用：10难度：0.8

  解析

• 3．不等式x+3＞0的解集是（　　）

  A． x ＞ 1 3

  B．x＞3

  C．x＞-3

  D． x ＞ - 1 3
  组卷：99引用：1难度：0.5

  解析

• 4．方程x²-3x-1=0的根的情况是（　　）

  A．没有实数根	B．有一个实数根
  C．有两个相等的实数根	D．有两个不相等的实数根
  组卷：201引用：1难度：0.8

  解析

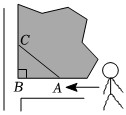• 5．如图，某小区的一块草坪旁边有一条直角小路，社区为了方便群众进行核酸采集，沿AC修了一条近路，已知AB=80米，新修小路与AB的夹角∠CAB为40°，则走这条近路AC的长可以表示为（　　）米．

  A．80sin40°

  B．80cos40°

  C． 80 sin 40 °

  D． 80 cos 40 °
  组卷：215引用：5难度：0.5

  解析

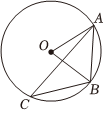• 6．如图，OA、OB是⊙O的半径，△ABC的顶点C在⊙O上，且点A、C在OB的异侧．若∠BAO=55°，则∠ACB的大小是（　　）

  A．35°

  B．45°

  C．55°

  D．70°
  组卷：175引用：2难度：0.6

  解析

• 7．尺规作图：作一个角等于已知角．操作过程如下：如图①，已知：∠AOB．
  求作：
  作法：（1）如图②，以点①为圆心，任意长为半径画弧，交OA，OB于C，D；
  （2）作射线O'A′，以点O'为圆心，②长为半径画弧，交O'A'于点C'：
  （3）以点C′圆心，③为半径画弧，与第（2）步中所画的弧相交于点D′；
  （4）经过点D'画射线O'B'，则∠A′O′B′=∠AOB．
  连结CD、C'D′．根据以上作法证得△C'O′D′≌△COD（④填理论依据）．根据以上作图和求证过程完成以上填空，题中符号代表的内容错误的是（　　）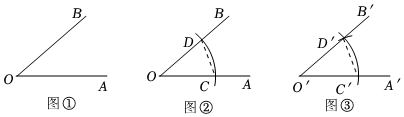
  

  A．①表示O	B．②表示OC或OD
  C．③表示CD	D．④表示SAS
  组卷：127引用：1难度：0.6

  解析

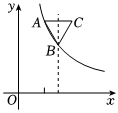• 8．如图，在平面直角坐标系中，△ABC在第一象限内，边AC与x轴平行，点A，B均在函数y=

  k

  x

  （x＞0）的图象上．若A，B两点的纵坐标分别为3，2，且AB=AC，△ABC的面积为

  5

  4

  ，则k值为（　　）

  A．3

  B．6

  C．9

  D．12
  组卷：241引用：1难度：0.5

  解析

三、解答题（本大题10小）题，共78分）

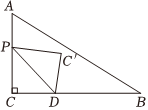• 23．如图，在△ABC中，∠C=90°，AC=2，BC=3，点D在边BC上，且CD=1．点P从点C出发，沿CA-AB方向匀速运动到终点B，在CA、AB上的速度分别是每秒1个单位长度和每秒

  13

  个单位长度．当点P不与△ABC的顶点重合时，连结DP，作点C关于直线DP的对称点C，连结PC′、DC′．设点P的运动时间为t秒．
  （1）AB=

  ．
  （2）用含t的代数式表示AP的长．
  （3）当点C′、B、P共线时，求四边形CDC′P的面积．
  （4）当C′D与△ABC的边AC或BC垂直时，直接写出此时t的值．
  组卷：177引用：2难度：0.3

  解析

• 24．在平面直角坐标系中，抛物线 y=x²+bx+c 经过点A（0，3），其对称轴为直线x=3，点B在该抛物线上，其横坐标为m.以点B为对称中心，作正方形PQMN，使PQ⊥x轴，且点P的横坐标为1．
  （1）求该抛物线对应的函数关系式．
  （2）当点B与点A重合时，求抛物线的顶点到正方形PQMN垂直于y轴的边的最短距离．
  （3）当点B在第四象限时，若抛物线与正方形PQMN的某一条边或一组邻边只有两个公共点，且这两个公共点的纵坐标之和为-8，求m的值．
  （4）当抛物线在正方形PQMN内部的部分对应的函数值y随x的增大而减小或y随x的增大而增大时，直接写出m的取值范围．
  组卷：166引用：1难度：0.1

  解析