2023-2024学年云南省曲靖市民族中学高一(下)第一次月考数学试卷
发布:2025/10/31 14:0:30
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.在边长为2的正三角形ABC中,
=( )AB•AC组卷:178引用:6难度:0.9 -
2.已知向量
,a不共线,且b=AB+4a,b=-BC+9a,b=3CD-a,则一定共线的三点是( )b组卷:139引用:6难度:0.9 -
3.已知函数
(a,b∈R)且f(lglog310)=5,则f(lglg3)=( )f(x)=atanx+b3x+4组卷:131引用:1难度:0.7 -
4.已知向量
与向量a的夹角为120°,b,则|a|=|b|=1=( )|a+2b|组卷:217引用:4难度:0.7 -
5.已知sin(θ-
)=π12,则sin(2θ+13)=( )π3组卷:363引用:9难度:0.7 -
6.已知函数f(x)定义域为I,M为常数,则“∀x∈I,f(x)≤M”是“M为f(x)在I上最大值”的( )
组卷:201引用:6难度:0.9 -
7.已知集合A={x|x-1>0},B={x|x2-2x≤0},则A∩B=( )
组卷:248引用:7难度:0.8 -
8.要得到函数y=sin(2x-
)的图象,只需将函数y=sin2x的图象( )π3组卷:1609引用:31难度:0.9
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
-
9.已知a>0,b>0,且a+b=1,则( )
组卷:406引用:30难度:0.6 -
10.已知函数
,则下列结论正确的是( )f(x)=tan(12x-π4)组卷:218引用:1难度:0.7 -
11.正方体ABCD-A1B1C1D1的棱长为2,MN是正方体内切球的直径,P为正方体表面上的动点,则
的值可以为( )PM•PN组卷:15引用:1难度:0.6
三、填空题:本题共3小题,每小题5分,共15分。
-
12.已知定义在R上的函数f(x)满足f(1+x)+f(1-x)=0,且f(x-1)关于x=1对称,当x∈[0,1]时,f(x)=ax2+b.若f(0)+f(3)=2,则
=.f(72)组卷:19引用:2难度:0.5 -
13.已知一扇形的周长为6,则当该扇形的面积取得最大时,圆心角的弧度数为 .
组卷:78引用:1难度:0.7 -
14.已知函数f(x)=e-x+lnx(e是自然对数的底数),若实数x0是方程f(x)=0的解,且0<x1<x0<x2,则f(x1)f(x2)(填“>”,“≥”,“<”,“≤”).
组卷:26引用:1难度:0.7
四、解答题:本题共5小题,共77分。解答应写出必要的文字说明、证明过程及演算步骤。
-
15.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π)在一个周期内,当
时,y取最小值-3;当x=π6时,y最大值3.x=2π3
(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)在区间上的最值.[π2,π]组卷:30引用:5难度:0.5 -
16.已知角α为锐角,
,且满足π2<β-α<π,tanα2=13.sin(β-α)=7210
(1)证明:;0<α<π4
(2)求β.组卷:97引用:2难度:0.5 -
17.已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个不同实数根.
(1)是否存在实数k,使成立?若存在,求出k的值;若不存在,请说明理由;(2x1-x2)(x1-2x2)=34
(2)求使的值为整数的实数k的整数值.x1x2+x2x1-2组卷:32引用:4难度:0.6 -
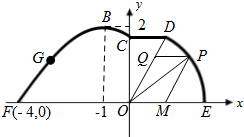 18.如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧.ˆDE
18.如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧.ˆDE
(1)求曲线段FGBC的函数表达式;
(2)曲线段FGBC上的入口G距海岸线EF最近距离为1千米,现准备从入口G修一条笔直的景观路到O,求景观路GO长;
(3)如图,在扇形ODE区域内建一个平行四边形休闲区OMPQ,平行四边形的一边在海岸线EF上,一边在半径OD上,另外一个顶点P在圆弧上,且∠POE=θ,求平行四边形休闲区OMPQ面积的最大值及此时θ的值.ˆDE组卷:333引用:4难度:0.3 -
19.已知点A(1,2)和向量
=(-3,4),求点B的坐标,使得向量AB∥a,且|AB|等于|a|的2倍.a组卷:12引用:1难度:0.5


