2023-2024学年山东省德州市宁津县育新中学八年级（上）月考数学试卷（10月份）
发布：2024/9/21 3:0:11
一、选择题（每题4分，共48分）
-
1．若一个三角形的三边长分别为2，6，a,则a的值可能是（ ）
组卷：110引用：6难度：0.8 -
2．画△ABC中AB边上的高，下列画法中正确的是（ ）
组卷：4306引用：62难度：0.9 -
3．如果等腰三角形的两边长是6cm和3cm,那么它的周长是（ ）
组卷：386引用：61难度：0.9 -
4．如果从一个n边形的一个顶点出发，最多能引出6条对角线，那么这个n边形的内角和是（ ）
组卷：142引用：9难度：0.7 -
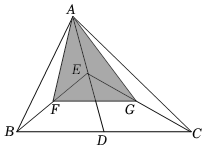5．如图，△ABC的面积是24，点D、E、F、G分别是BC、AD、BE、CE的中点，则△AFG的面积是（ ）组卷：533引用：4难度：0.7 -
6．根据下列条件能判定△ABC是直角三角形的有（ ）
①∠A+∠B=∠C，②，③∠A：∠B：∠C=5：2：3，④∠A=2∠B=3∠C．∠A=12∠B=13∠C组卷：1310引用：8难度：0.6 -
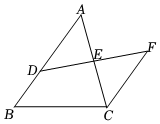7．如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，若AB=4，CF=3，则BD的长是（ ）组卷：5185引用：64难度：0.7 -
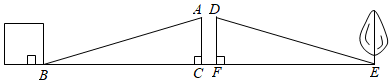
8．如图，抗日战争期间，为了炸毁敌人的碉堡，需要测出我军阵地与敌人碉堡的距离．我军战士想到一个办法，他先面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部点B；然后转过身保持刚才的姿势，这时视线落在了我军阵地的点E上；最后，他用步测的办法量出自己与E点的距离，从而推算出我军阵地与敌人碉堡的距离，这里判定△ABC≌△DEF的理由可以是（ ）
组卷：902引用：10难度：0.8
三、解答题（共78分）
-
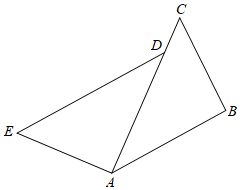24．如图，已知D是AC上一点，AB=DA，AB+DC=ED，AE=BC．
（1）求证：△ABC≌△DAE；
（2）若∠BAE=125°，求∠DCB的度数．组卷：652引用：4难度：0.4 -
25．央视科教频道播放的《被数学选中的人》节目中说到，“数学区别于其它学科最主要的特征是抽象与推理”．几何学习尤其需要我们从复杂的问题中进行抽象，形成一些基本几何模型，用类比等方法，进行再探究、推理，以解决新的问题．
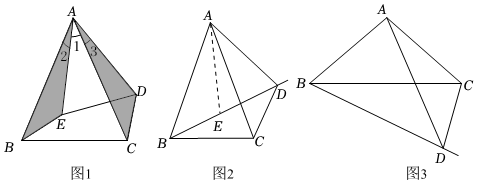
（1）【模型探究】如图1，△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，连接BE，CD．这一图形称“手拉手模型”．
求证△ABE≌△ACD，请你完善下列过程．
证明：∵∠BAC=∠DAE，
∴∠BAC-∠1=∠DAE-∠1（ ）①．
即∠2=∠3．
在△ABE和△ACD中，AB=AC（ㅤㅤ）②（ㅤㅤ）③
∴△ABE≌△ACD（ ）④．
（2）【模型指引】如图2，△ABC中，AB=AC，∠BAC=40°，以B为端点引一条与腰AC相交的射线，在射线上取点D，使∠ADB=∠ACB，求∠BDC的度数．
小亮同学通过观察，联想到手拉手模型，在BD上找一点E，使AE=AD，最后使问题得到解决．请你帮他写出解答过程．
（3）【拓展延伸】如图3，△ABC中，AB=AC，∠BAC为任意角度，若射线BD不与腰AC相交，而是从端点B向右下方延伸．仍在射线上取点D，使∠ADB=∠ACB，试判断∠BAC与∠BDC有何数量关系？并写出简要说明．组卷：686引用：4难度：0.5
