2022-2023学年福建省福州市八县（市）协作校高二（下）期末数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x∈Z|x²-4≤0}，B={1，2}，则A∪B=（　　）

  A．{0，1，2}	B．{-2，-1，0，1，2}
  C．{-2，-1，1，2}	D．{-1，0，1，2}
  组卷：73引用：2难度：0.8

  解析

• 2．若复数z满足z•（1+i）=2，则复数z的虚部为（　　）

  A．-i

  B．i

  C．-1

  D．1
  组卷：24引用：1难度：0.8

  解析

• 3．已知sinα+

  2

  cosα=0，则tan2α=（　　）

  A．2 2

  B．-2 2

  C． 2

  D． 2 4
  组卷：189引用：3难度：0.7

  解析

• 4．南宋数学家杨辉所著的《详解九章算法•商功》中出现了如图所示的形状，后人称之为“三角垛”．“三角垛”的最上层（即第一层）有1个球，第二层有3个球，第三层有6个球，…．若“三角垛”从第一层到第n层的各层的球数构成一个数列{a_n}，则（　　）

  A．a6-a5=5	B．a10=45
  C．an+an+2=2an+1	D．an+1-an=n+1
  组卷：38引用：1难度：0.8

  解析

• 5．已知p：a+b≤6，q：ab≤9，则p是q的（　　）条件．

  A．充分不必要	B．必要不充分
  C．充分必要	D．既不充分也不必要
  组卷：79引用：1难度：0.8

  解析

• 6．已知四边形ABCD是平行四边形，

  AE

  =

  2

  EB

  ，若EC与BD交于点O，且

  EO

  =

  λ

  AB

  +

  1

  4

  ED

  ，则λ=（　　）

  A． 1 4

  B． 3 8

  C． 1 2

  D． 3 4
  组卷：66引用：1难度：0.7

  解析

• 7．设点F₁，F₂分别是椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦点，点M，N在C上（M位于第一象限），且点M，N关于原点对称，若|MN|=|F₁F₂|，|NF₂|=3|MF₂|，则C的离心率为（　　）

  A． 10 8

  B． 10 4

  C． 5 8

  D． 5 5 8
  组卷：188引用：1难度：0.5

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

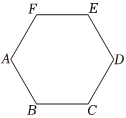• 21．如图，正六边形ABCDEF的边长为4．已知双曲线Γ的焦点分别为A，D，两条渐近线分别为直线BE，CF．
  （1）建立适当的平面直角坐标系，求Γ的方程；
  （2）过点A的直线l与Γ交于P，Q两点，

  AP

  =

  λ

  AQ

  （

  λ

  ≠

  -

  1

  ）

  ，若点M满足

  PM

  =

  λ

  MQ

  ，证明：点M在一条定直线上．
  组卷：23引用：1难度：0.5

  解析

• 22．已知函数f（x）=ax+

  b

  x

  -lnx,其中a,b∈R．
  （1）若b=0，讨论函数f（x）的单调性；
  （2）已知x₁，x₂是函数f（x）的两个零点，且x₁＜x₂，证明：x₂（ax₁-1）＜b＜x₁（ax₂-1）．
  组卷：48引用：1难度：0.5

  解析