当前位置：试卷中心 > 试卷详情

2023-2024学年黑龙江省大庆市高一（下）期末数学试卷

发布：2025/10/31 5:0:23

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1．已知函数
f
（
x
）
=
2
sin
（
ωx
+
π
3
）
（
ω
＞
0
）
且满足f（
2
π
3
-x）=f（x-
π
6
），则ω的最小值为（　　）
A．
2
3
B．
1
2
C．1 D．2
组卷：464引用：8难度：0.6
2．已知空间向量
a
=
（
3
，
2
，
5
）
，
b
=
（
1
，
x
,-
1
）
，且
a
与
b
垂直，则x等于（　　）
A．4 B．1 C．3 D．2
组卷：30引用：6难度：0.8
3．已知
cos
（
α
-
π
2
）
=
-
3
5
，
α
∈
（
-
π
2
，
0
）
，则sin2α的值为（　　）
A．
1
25
B．
24
25
C．-
24
25
D．-
1
25
组卷：157引用：1难度：0.7
4．已知函数f（x）为R上的可导函数，其导函数为f'（x），且f（x）=
3
f
′
（
π
6
）
•
sinx
+
cosx
，在△ABC中，f（A）=f'（B）=1，则△ABC的形状为（　　）
A．等腰锐角三角形 B．直角三角形
C．等边三角形 D．等腰钝角三角形
组卷：58引用：5难度：0.7
5．已知直线l与平面α相交，则下列命题中，正确的个数为（　　）
①平面α内的所有直线均与直线l异面；
②平面α内存在与直线l垂直的直线；
③平面α内不存在直线与直线l平行；
④平面α内所有直线均与直线l相交．
A．1 B．2 C．3 D．4
组卷：152引用：3难度：0.7
6．△ABC中∠C=90°，AC=2，P为线段BC上任一点，则
AP
•
AC
=（　　）
A．2 B．4 C．8 D．不确定
组卷：111引用：3难度：0.8
7．已知向量
a
=
（
2
，
3
）
，
b
=
（
-
1
，
3
）
，则
a
在
b
上的投影向量为（　　）
A．
（
-
1
4
，
3
4
）
B．
（
1
4
，-
3
4
）
C．
（
1
2
，-
3
2
）
D．
（
-
1
2
，
3
2
）
组卷：493引用：9难度：0.5
8．系统找不到该试题

二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对的得6分，部分选对的得2分，有选错的得0分。

9．一组数据x₁，x₂，…，x₁₀是公差为-1的等差数列，若去掉首末两项x₁，x₁₀后，则（　　）
A．平均数变大 B．中位数没变 C．方差变小 D．极差没变
组卷：165引用：2难度：0.8
10．关于复数，给出下列命题正确的是（　　）
A．3＞3i B．16＞（4i）² C．2+i＞1+i D．|2+3i|＞|2+i|．
组卷：4引用：4难度：0.7
11．攒尖是我国古代建筑中屋顶的一种结构形式，宋代称为最尖，清代称攒尖，通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖，也有单檐和重檐之分，多见于亭阁式建筑，园林建筑．下面以四角攒尖为例，如图，它的屋顶部分的轮廓可近似看作一个正四棱锥．已知此正四棱锥的侧棱与底面所成角的正切值近似为
6
6
，侧棱长近似为
21
米，则下列结论正确的是（　　）
A．正四棱锥的底面边长近似为3米
B．正四棱锥的高近似为
3
米
C．正四棱锥的侧面积近似为
48
3
平方米
D．正四棱锥的体积近似为
12
3
立方米
组卷：58引用：2难度：0.5

三、填空题：本题共3小题，每小题5分，共15分。

12．若一个扇形的圆心角是45°，面积为2π，则这个扇形的半径为
．
组卷：69引用：3难度：0.7
13．2023年3月，某市为创建文明城市，随机从某小区抽取10位居民调查他们对自己目前生活状态的满意程度，该指标数越接近10表示满意程度越高．他们的满意度指标数分别是8，5，6，6，9，8，9，7，10，10，则这组数据的30%分位数是
．
组卷：13引用：2难度：0.8
14．如图，半球内有一内接正方体，正方体的一个面在半球的底面圆内，若正方体的棱长为2，则半球的表面积为
．
组卷：103引用：1难度：0.6

四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。

15．随机观测生产某种零件的某工作厂25名工人的日加工零件个数（单位：件），获得数据如下：30，42，41，36，44，40，37，37，25，45，29，43，31，36，49，34，33，43，38，42，32，34，46，39，36．根据上述数据得到样本的频率分布表如下：
分组频数频率
[25，30] 3 0.12
（30，35] 5 0.20
（35，40] 8 0.32
（40，45] n₁ f₁
（45，50] n₂ f₂
（1）确定样本频率分布表中n₁，n₂，f₁和f₂的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）根据样本频率分布直方图，求在该厂任取4人，至少有1人的日加工零件数落在区间（30，35]的概率．
组卷：1150引用：23难度：0.3
16．已知函数f（x）=|2x-3|+1．
（Ⅰ）求不等式f（x）≥x的解集；
（Ⅱ）若关于x的不等式f（x）-2|x+1|≤a无解，求实数a的取值范围．
组卷：60引用：5难度：0.5
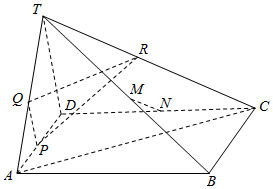17．已知四棱锥T-ABCD的底面是平行四边形，平面α与直线AD，TA，TC分别交于点P，Q，R且
AP
AD
=
TQ
TA
=
CR
CT
=x,点M在直线TB上，N为CD的中点，且直线MN∥平面α．
（Ⅰ）设
TA
=
a
，
TB
=
b
，
TC
=
c
，试用基底{
a
，
b
，
c
}表示向量
TD
；
（Ⅱ）证明：四面体TABC中至少存在一个顶点，从其出发的三条棱能够组成一个三角形；
（Ⅲ）证明：对所有满足条件的平面α，点M都落在某一条长为
5
2
TB的线段上．
组卷：188引用：6难度：0.5
18．计算（5-6i）+（-2-i）-（3+4i）．
组卷：11引用：2难度：0.7
19．如图，A、B是海岸线OM、ON上的两个码头，海中小岛有码头Q到海岸线OM、ON的距离分别为2km、
7
10
5
km
．测得tan∠MON=-3，OA=6km.以点O为坐标原点，射线OM为x轴的正半轴，建立如图所示的直角坐标系．码头Q在第一象限，且三个码头A、B、Q均在一条航线上．
（1）求码头Q点的坐标；
（2）海中有一处景点P（设点P在平面xOy内，PQ⊥OM，且PQ=6km），游轮无法靠近．求游轮在水上沿旅游线AB航行时离景点P最近的点C的坐标．
组卷：140引用：4难度：0.6

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．等腰锐角三角形	B．直角三角形
C．等边三角形	D．等腰钝角三角形

分组	频数	频率
[25，30]	3	0.12
（30，35]	5	0.20
（35，40]	8	0.32
（40，45]	n₁	f₁
（45，50]	n₂	f₂

2023-2024学年黑龙江省大庆市高一（下）期末数学试卷

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1．已知函数f（x）=2sin（ωx+π3）（ω＞0）且满足f（2π3-x）=f（x-π6），则ω的最小值为（ ）

2．已知空间向量a=（3，2，5），b=（1，x,-1），且a与b垂直，则x等于（ ）

3．已知cos（α-π2）=-35，α∈（-π2，0），则sin2α的值为（ ）

4．已知函数f（x）为R上的可导函数，其导函数为f'（x），且f（x）=3f′（π6）•sinx+cosx，在△ABC中，f（A）=f'（B）=1，则△ABC的形状为（ ）

5．已知直线l与平面α相交，则下列命题中，正确的个数为（ ）①平面α内的所有直线均与直线l异面；②平面α内存在与直线l垂直的直线；③平面α内不存在直线与直线l平行；④平面α内所有直线均与直线l相交．

6．△ABC中∠C=90°，AC=2，P为线段BC上任一点，则AP•AC=（ ）

7．已知向量a=（2，3），b=（-1，3），则a在b上的投影向量为（ ）

二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对的得6分，部分选对的得2分，有选错的得0分。

9．一组数据x1，x2，…，x10是公差为-1的等差数列，若去掉首末两项x1，x10后，则（ ）

10．关于复数，给出下列命题正确的是（ ）

三、填空题：本题共3小题，每小题5分，共15分。

12．若一个扇形的圆心角是45°，面积为2π，则这个扇形的半径为 ．

14．如图，半球内有一内接正方体，正方体的一个面在半球的底面圆内，若正方体的棱长为2，则半球的表面积为 ．

四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。

16．已知函数f（x）=|2x-3|+1．（Ⅰ）求不等式f（x）≥x的解集；（Ⅱ）若关于x的不等式f（x）-2|x+1|≤a无解，求实数a的取值范围．

18．计算（5-6i）+（-2-i）-（3+4i）．

1．已知函数
f
（
x
）
=
2
sin
（
ωx
+
π
3
）
（
ω
＞
0
）
且满足f（
2
π
3
-x）=f（x-
π
6
），则ω的最小值为（　　）

2．已知空间向量
a
=
（
3
，
2
，
5
）
，
b
=
（
1
，
x
,-
1
）
，且
a
与
b
垂直，则x等于（　　）

3．已知
cos
（
α
-
π
2
）
=
-
3
5
，
α
∈
（
-
π
2
，
0
）
，则sin2α的值为（　　）

4．已知函数f（x）为R上的可导函数，其导函数为f'（x），且f（x）=
3
f
′
（
π
6
）
•
sinx
+
cosx
，在△ABC中，f（A）=f'（B）=1，则△ABC的形状为（　　）

5．已知直线l与平面α相交，则下列命题中，正确的个数为（　　）
①平面α内的所有直线均与直线l异面；
②平面α内存在与直线l垂直的直线；
③平面α内不存在直线与直线l平行；
④平面α内所有直线均与直线l相交．

6．△ABC中∠C=90°，AC=2，P为线段BC上任一点，则
AP
•
AC
=（　　）

7．已知向量
a
=
（
2
，
3
）
，
b
=
（
-
1
，
3
）
，则
a
在
b
上的投影向量为（　　）

9．一组数据x₁，x₂，…，x₁₀是公差为-1的等差数列，若去掉首末两项x₁，x₁₀后，则（　　）

10．关于复数，给出下列命题正确的是（　　）

12．若一个扇形的圆心角是45°，面积为2π，则这个扇形的半径为
．

14．如图，半球内有一内接正方体，正方体的一个面在半球的底面圆内，若正方体的棱长为2，则半球的表面积为
．

16．已知函数f（x）=|2x-3|+1．
（Ⅰ）求不等式f（x）≥x的解集；
（Ⅱ）若关于x的不等式f（x）-2|x+1|≤a无解，求实数a的取值范围．