2022-2023学年河南省洛阳市伊滨区九年级（上）第二次质检数学试卷

一、选择题（每小题3分，共30分）

• 1．下列图形既是中心对称图形也是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1220引用：18难度：0.9

  解析

• 2．抛物线的函数表达式为y=3（x-2）²+1，若将x轴向上平移2个单位长度，将y轴向左平移3个单位长度，则该抛物线在新的平面直角坐标系中的函数表达式为（　　）

  A．y=3（x+1）2+3	B．y=3（x-5）2+3
  C．y=3（x-5）2-1	D．y=3（x+1）2-1
  组卷：3943引用：42难度：0.6

  解析

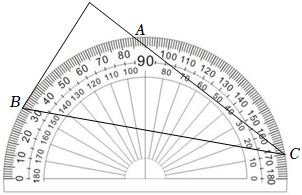• 3．将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A，B的读数分别为86°，30°，则∠ACB的度数是（　　）

  A．28°

  B．30°

  C．36°

  D．56°
  组卷：2962引用：27难度：0.5

  解析

• 4．如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C，连接AA'，若∠1=25°．则∠BAA'的度数是（　　）

  A．55°

  B．60°

  C．65°

  D．70°
  组卷：253引用：10难度：0.7

  解析

• 5．已知（0，y₁），（

  3

  ，y₂），（3，y₃）是抛物线y=ax²-4ax+1（a是常数，且a＜0）上的点，则（　　）

  A．y1＞y2＞y3

  B．y3＞y2＞y1

  C．y2＞y3＞y1

  D．y2＞y1＞y3
  组卷：717引用：4难度：0.6

  解析

• 6．若点O是△ABC的外心，且∠BOC=50°，则∠BAC的度数为（　　）

  A．25°

  B．130°

  C．25°或130°

  D．25°或155°
  组卷：42引用：2难度：0.7

  解析

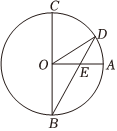• 7．如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上（不与点A，点C重合），BD与OA交于点E．设∠AED=α，∠AOD=β，则（　　）

  A．3α+β=180°

  B．2α+β=180°

  C．3α-β=90°

  D．2α-β=90°
  组卷：6557引用：34难度：0.8

  解析

三、解答题（本大题共8小题，共75分）

• 22．如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．
  （1）观察猜想：图1中，线段PM与PN的数量关系是

  ，位置关系是

  ；
  （2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；
  （3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值．
  
  组卷：6320引用：50难度：0.1

  解析

• 23．在平面直角坐标系中，二次函数y=ax²+bx+2的图象与x轴交于A（-3，0），B（1，0）两点，与y轴交于点C．
  （1）求这个二次函数的关系解析式，x满足什么值时y＜0？
  （2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP面积最大？若存在，求出点P的坐标；若不存在，说明理由；
  （3）点M为抛物线上一动点，在x轴上是否存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由．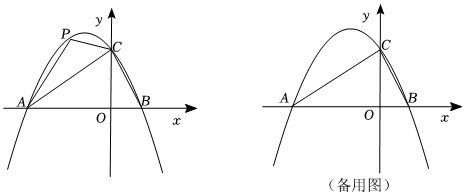
  
  组卷：1610引用：7难度：0.4

  解析