当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省连云港市东海县高一（上）期中数学试卷

发布：2024/9/2 4:0:8

1．已知全集U={1，2，3，5}，M={1，2}，N={3，4}，（∁_UM）∪N=（　　）
A．{4} B．{4，5} C．{3，4，5} D．{1，2，3，4，5}
组卷：58引用：5难度：0.7
解析
2．函数
f
（
x
）
=
x
+
1
2
x
的定义域是（　　）
A．（-∞，-1）∪（-1，0） B．[-1，+∞）
C．[-1，0） D．[-1，0）∪（0，+∞）
组卷：78引用：10难度：0.9
解析
3．设a＞0，b＞0，则“ab＞1”是“a+b＞1”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：26引用：3难度：0.8
解析
4．已知函数
f
（
x
）
=
x
3
+
1
，
x
＜
1
x
2
-
ax
,
x
≥
1
，若f（f（0））=-2，实数a=（　　）
A．1 B．2 C．3 D．4
组卷：183引用：12难度：0.9
解析
5．若一次函数f（x）=ax+b有一个零点2，则函数g（x）=bx²-ax的图象可能是（　　）
A． B． C． D．
组卷：75引用：5难度：0.7
解析
6．设a=log₂3，b=log₃5，c=
3
2
，则（　　）
A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b
组卷：344引用：4难度：0.7
解析
7．已知正数x,y满足x+y=1，则下列说法错误的是（　　）
A．
1
x
+
1
y
≥
4
B．
x
2
+
y
2
≤
1
2
C．
y
x
+
x
y
≥
2
D．
x
+
y
≤
2
组卷：15引用：2难度：0.6
解析

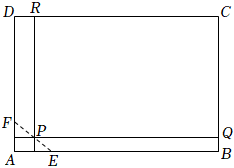21．如图，某房地产开发公司要在矩形地块ABCD上规划出一块矩形地块PQCR建造住宅区．为了保护文物，住宅区不能超越文物保护区△AEF的界线EF．由实地测量知，AB=200m,AD=160m,AE=60m,AF=40m.问：怎样设计矩形住宅区的长和宽，才能使其面积最大？最大面积是多少？
组卷：19引用：3难度：0.4
解析
22．已知f（x）=x|x-2m|+x,m∈R．
（1）判断f（x）的奇偶性并说明理由；
（2）当x∈[0，1]时，f（x）的最大值为2，求m的值．
组卷：46引用：2难度：0.5
解析