2022-2023学年江苏省宿迁市高二（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每个小题给出的四个选项中，只有一项是符合题目要求的．

• 1．设n∈N₊，化简

  C

  0

  n

  +

  C

  1

  n

  6

  1

  +

  C

  2

  n

  6

  2

  +

  C

  3

  n

  6

  3

  +

  ⋯

  +

  C

  n

  n

  6

  n

  =（　　）

  A．6n

  B．6n-1

  C．7n

  D．7n-1
  组卷：50引用：1难度：0.8

  解析

• 2．已知平面α的一个法向量为

  n

  =

  （

  1

  ，-

  1

  ，

  2

  ）

  ，

  AB

  =

  （

  -

  1

  ，

  1

  ，-

  2

  ）

  ，则AB所在直线l与平面α的位置关系为（　　）

  A．l⊥α	B．l⊂α
  C．l∥α	D．l与α相交但不垂直
  组卷：98引用：5难度：0.7

  解析

• 3．已知向量

  a

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，则向量

  b

  在向量

  a

  上的投影向量为（　　）

  A．（0，-1，-1）

  B．（-1，0，-1）

  C． （ 0 ， 1 2 ， 1 2 ）

  D． （ 1 2 ， 0 ， 1 2 ）
  组卷：212引用：8难度：0.8

  解析

• 4．由0，1，2，3，5组成的无重复数字的五位偶数共有（　　）

  A．36个

  B．42个

  C．48个

  D．120个
  组卷：264引用：8难度：0.9

  解析

• 5．已知空间四面体OABC中，对空间内任一点M，满足

  OM

  =

  1

  4

  OA

  +

  1

  6

  OB

  +

  λ

  OC

  ，下列条件中能确定点M，A，B，C共面的是（　　）

  A． λ = 1 2

  B． λ = 1 3

  C． λ = 5 12

  D． λ = 7 12
  组卷：576引用：5难度：0.7

  解析

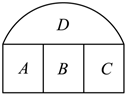• 6．如图，提供4种不同的颜色给图中A，B，C，D四块区域涂色，若相邻的区域不能涂同一种颜色，则不同的涂法共有（　　）种

  A．12

  B．36

  C．48

  D．72
  组卷：237引用：4难度：0.5

  解析

• 7．当n∈N时，将三项式（x²+x+1）ⁿ展开，可得到如图所示的三项展开式和“广义杨辉三角形”：
  （x²+x+1）⁰=1
  （x²+x+1）¹=x²+x+1
  （x²+x+1）²=x⁴+2x³+3x²+2x+1
  （x²+x+1）³=x⁶+3x⁵+6x⁴+7x³+6x²+3x+1
  （x²+x+1）⁴=x⁸+4x⁷+10x⁶+16x⁵+19x⁴+16x³+10x²+4x+1
  ……
  
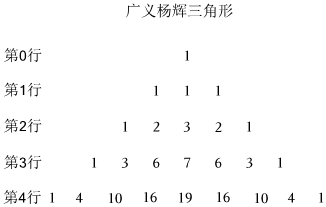
  若在（1+ax）（x²+x+1）⁵的展开式中，x⁸的系数为75，则实数a的值为（　　）

  A．1

  B．-1

  C．2

  D．-2
  组卷：89引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．（1）3个不同的小球放入编号为1，2，3，4的4个盒子中，一共有多少种不同的放法？
  （2）3个不同的小球放入编号为1，2，3，4的4个盒子中，恰有2个空盒的放法共有多少种？
  组卷：205引用：3难度：0.8

  解析

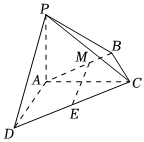• 22．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA=60°，AP=AD=AC=2，E为CD的中点，M在AB上，且

  AM

  =

  2

  MB

  ．
  （1）求证：EM∥平面PAD；
  （2）求平面PAD与平面PBC夹角的正弦值；
  （3）点F是线段PD上异于两端点的任意一点，若满足异面直线EF与AC所成角为45°，求AF的长．
  组卷：55引用：1难度：0.5

  解析