2022-2023学年北京市人大附中朝阳分校七年级（下）限时作业数学试卷（五）

一、选择题（下列各题，每题只有一个符合题意的答案）

• 1．

  1

  4

  的算术平方根为（　　）

  A． 1 16

  B． ± 1 2

  C． 1 2

  D．- 1 2
  组卷：659引用：27难度：0.9

  解析

• 2．北京2022年冬奥会会徽是以汉字“冬”为灵感来源设计的．在选项的四个图中，能由如图经过平移得到的是（　　）

  A．

  B．

  C．

  D．
  组卷：621引用：48难度：0.8

  解析

• 3．在0.515115111…（每两个5之间依次增加1），

  49

  100

  ，0.2，

  7

  ，

  131

  11

  ，

  3

  27

  ，

  π

  2

  中，无理数的个数是（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：159引用：1难度：0.9

  解析

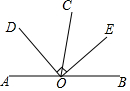• 4．如图，O为直线AB上一点，OE平分∠BOC，OD⊥OE于点O，若∠BOC=80°，则∠AOD的度数是（　　）

  A．70°

  B．50°

  C．40°

  D．35°
  组卷：1011引用：12难度：0.8

  解析

• 5．下列命题中，真命题是（　　）

  A．两个锐角的和一定是钝角

  B．相等的角是对顶角

  C．带根号的数一定是无理数

  D．垂线段最短
  组卷：167引用：12难度：0.8

  解析

• 6．如图，在数轴上，与表示

  14

  的点最接近的点是（　　）

  A．点P

  B．点Q

  C．点M

  D．点N
  组卷：31引用：2难度：0.8

  解析

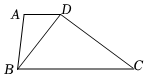• 7．如图，AD∥BC，∠C=30°，∠ADB：∠BDC=1：2，则∠ADB的度数是（　　）

  A．45°

  B．30°

  C．50°

  D．36°
  组卷：227引用：4难度：0.5

  解析

三、解答题

• 22．线段AB与线段CD互相平行，P是平面内的一点，且点P不在直线AB，CD上，连接PA，PD，射线AM，DN分别是∠BAP和∠CDP的平分线．
  （1）若点P在线段AD上，如图1，
  ①依题意补全图1；
  ②判断AM与DN的位置关系，并证明；
  （2）是否存在点P，使AM⊥DN？若存在，直接写出点P的位置；若不存在，说明理由．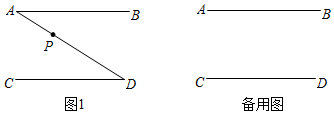
  
  组卷：745引用：9难度：0.6

  解析

• 23．欧几里得《原本》中给出

  2

  不是有理数的证明方法．
  假设

  2

  是有理数，那么存在两个互质的正整数p,q,使得

  2

  =

  p

  q

  ，于是

  p

  =

  2

  q

  ．两边平方得p²=2q²．由2q²是偶数，可得p²是偶数．而只有偶数的平方才是偶数，所以p也是偶数．因此可设p=2s,代入上式，得4s²=2q²，即q²=2s²．
  所以q也是偶数．这样，p和q都是偶数，不互质，这与假设p,q互质矛盾．说明

  2

  不能写成分数的形式，即．

  2

  不是有理数．
  请你阅读上述材料，用类似的方法，证明

  3

  2

  不是有理数．
  组卷：104引用：1难度：0.2

  解析