当前位置：试卷中心 > 试卷详情

2022-2023学年天津市南开区高一（下）期末数学试卷

发布：2024/5/27 8:0:10

1．从装有4个黑球、2个白球的袋中任取3个球，若事件A为“所取的3个球中至多有1个白球”，则与事件A互斥的事件是（　　）
A．所取的3个球中至少有一个白球
B．所取的3个球中恰有2个白球1个黑球
C．所取的3个球都是黑球
D．所取的3个球中恰有1个白球2个黑球
组卷：706引用：10难度：0.8
解析
2．设复数z=1-2i,则复数z的模为（　　）
A．1 B．10 C．3 D．
5
组卷：118引用：3难度：0.8
解析
3．已知
|
a
|
=
3
，
|
b
|
=
4
，且
a
与
b
的夹角θ=120°，则
a
•
b
等于（　　）
A．-6 B．6 C．
-
6
3
D．
6
3
组卷：296引用：5难度：0.8
解析
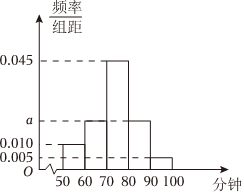4．某研究机构为了解某地年轻人的阅读情况，通过随机抽样调查了100位年轻人，对这些人每天的阅读时间（单位：分钟）进行统计，得到样本的频率分布直方图（如图所示），则a的值为（　　）
A．0.20 B．0.040 C．0.020 D．0.010
组卷：156引用：4难度：0.7
解析
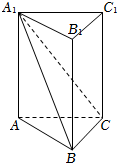5．如图，在正三棱柱ABC-A₁B₁C₁中，AB=2，AA₁=3，则四棱锥A₁-B₁C₁CB的体积是（　　）
A．2
3
B．2
10
C．
4
2
3
D．4
6
组卷：464引用：6难度：0.7
解析

6．某校高一年级随机抽取15名男生，测得他们的身高数据，如下表所示：

编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

身高 173 179 175 173 170 169 177 175 174 182 168 175 172 169 176

那么这组数据的第80百分位数是（　　）

A．170

B．175

C．176

D．176.5

组卷：133引用：2难度：0.7

19．已知△ABC的内角A，B，C的对边分别是a,b,c,且a=1，
sin
A
-
sin
C
=
b
a
+
c
（
sin
B
-
sin
C
）
．
（1）求角A；
（2）求△ABC周长的取值范围．
组卷：241引用：3难度：0.6
解析
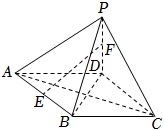20．如图，四棱锥P-ABCD的底面ABCD为菱形，PB=PD，E，F分别为AB和PD的中点．
（1）求证：EF∥平面PBC；
（2）求证：平面PBD⊥平面PAC．
组卷：2141引用：8难度：0.9
解析

编号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
身高	173	179	175	173	170	169	177	175	174	182	168	175	172	169	176