2022-2023学年青海省西宁市高一（下）期末数学试卷

一、选择题（本大题共8小题，每小题5分，共40分，每小题给出的四个选项中只有一个选项符合要求）

• 1．已知向量

  a

  =

  （

  2

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ）

  ，则

  a

  +

  b

  =（　　）

  A．（3，0）

  B．（3，1）

  C．（-1，2）

  D．（1，2）
  组卷：68引用：5难度：0.8

  解析

• 2．复数z在复平面内对应的点是（0，1），则复数

  1

  1

  -

  z

  =（　　）

  A． 1 + i 2

  B． - 1 + i 2

  C． - 1 - i 2

  D． 1 - i 2
  组卷：74引用：2难度：0.9

  解析

• 3．如表是校篮球队某队员若干场比赛的得分数据，则该队员得分的第40百分位数是（　　）
  

  每场比赛得分	3	6	7	10	11	13	30
  频数	2	1	2	3	1	1	1

  A．6

  B．7

  C．8

  D．10
  组卷：59引用：3难度：0.8

  解析

• 4．设m,n是两条不同的直线，α，β是两个不同的平面，下列命题中错误的是（　　）

  A．若m⊥α，m∥n,n∥β，则α⊥β

  B．若α∥β，m⊂α，则m∥β

  C．若m⊥n,m⊂α，n⊂β，则α⊥β

  D．若m∥n,α∥β，则m与α所成的角和n与β所成的角相等
  组卷：168引用：2难度：0.6

  解析

• 5．管理人员从一池塘内随机捞出40条鱼，做上标记后放回池塘．10天后，又从池塘内随机捞出70条鱼，其中有标记的有2条．根据以上数据可以估计该池塘内鱼的总条数是（　　）

  A．2800

  B．1800

  C．1400

  D．1200
  组卷：198引用：4难度：0.8

  解析

• 6．已知圆锥的底面半径为

  2

  ，其侧面展开图为一个半圆，则该圆锥的母线长为（　　）

  A．2

  B．2 2

  C．4

  D．4 2
  组卷：6708引用：44难度：0.8

  解析

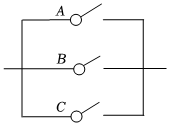• 7．如图所示，A，B，C表示3个开关，若在某段时间内它们正常工作的概率分别为0.9，0.8，0.8，则该系统的可靠性（3个开关只要一个开关正常工作即可靠）为（　　）

  A．0.504

  B．0.964

  C．0.994

  D．0.996
  组卷：37引用：3难度：0.7

  解析

四、解答题（本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤）

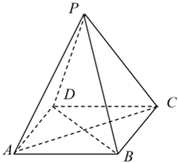• 21．如图，正四棱锥P-ABCD中．
  （1）求证：平面PAC⊥平面PBD；
  （2）若PA=2AB，求二面角B-PC-A的余弦值．
  组卷：102引用：2难度：0.5

  解析

• 22．已知锐角△ABC的内角A，B，C所对的边分别为a,b,c,向量

  m

  =

  （

  b

  ,

  sin

  B

  ）

  ，

  n

  =

  （

  2

  a

  ,

  3

  ）

  ，且

  m

  ∥

  n

  ．
  （1）求角A的大小；
  （2）若c=2，BC边上的中线AD长为

  3

  ，求b.
  组卷：274引用：5难度：0.6

  解析