2020-2021学年天津市河东区高二(上)期中数学试卷
发布:2025/10/29 16:0:44
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.在空间四边形ABCD中,
,AB=a,AC=b,点M在AC上,且AD=c,N为BD的中点,则AC=4MC=( )MN组卷:407引用:3难度:0.7 -
2.过点(1,0)且倾斜角为30°的直线被圆(x-2)2+y2=1所截得的弦长为( )
组卷:7引用:1难度:0.7 -
 3.国家体育场(鸟巢),是2008年北京奥运会的主体育场.在《通用技术》课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为40cm,短轴长为20cm,小椭圆的短轴长为10cm,则小椭圆的长轴长为( )cm.组卷:34引用:2难度:0.7
3.国家体育场(鸟巢),是2008年北京奥运会的主体育场.在《通用技术》课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为40cm,短轴长为20cm,小椭圆的短轴长为10cm,则小椭圆的长轴长为( )cm.组卷:34引用:2难度:0.7 -
4.设椭圆C1的离心率为
,焦点在x轴上且长轴长为26,若曲线C2上的点到C1的两个焦点的距离的差的绝对值为8,则曲线C2的标准方程为( )513组卷:363引用:10难度:0.9 -
5.P为抛物线y2=2px(p>0)上一点,点P到抛物线准线和对称轴的距离分别为10和6,则p=( )
组卷:360引用:4难度:0.7 -
6.如果AB<0,BC>0,那么直线Ax+By+C=0不经过( )
组卷:160引用:6难度:0.8 -
7.已知椭圆C:
=1(a>b>0)上有一异于顶点的点P,A,B分别是椭圆C的左、右顶点,且两直线PA,PB的斜率的乘积为-x2a2+y2b2,则椭圆C的离心率e为( )12组卷:755引用:4难度:0.6 -
8.已知空间向量
,a=(1,2,3),若b=(m,-1,n)a,则m+n=( )∥b组卷:749引用:8难度:0.8 -
9.若
构成空间的一个基底,则下列向量不共面的是( ){a,b,c}组卷:107引用:4难度:0.5 -
10.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在位置为B(2,4),若将军从点A(-2,0)处出发,河岸线所在直线方程为x-2y+8=0,则“将军饮马”的最短总路程为( )
组卷:365引用:5难度:0.8 -
11.在空间直角坐标系中,向量
,a=(2,-3,5),则向量b=(-2,4,5)=( )a+b组卷:653引用:2难度:0.9
二、填空题:本大题共8小题,每小题4分,共24分.
-
12.已知直线x+2y-3=0与椭圆
相交于A,B两点,且线段AB的中点在直线3x-4y+1=0上,则此椭圆的离心率为.x2a2+y2b2=1(a>b>0)组卷:540引用:5难度:0.5 -
13.正方体ABCD-A1B1C1D1的棱长为1,MN是正方体内切球的直径,P为正方体表面上的动点,则
•PM的最大值为.PN组卷:591引用:3难度:0.5 -
14.椭圆
的左焦点为F,直线x=m与椭圆相交于A,B两点,当△FAB的周长最大时,△FAB的面积为ab.若b=1,则椭圆的准线方程是.x2a2+y2b2=1(a>b>0)组卷:52引用:1难度:0.7 -
15.双曲线
的右焦点为F,双曲线C的一条渐近线与以OF为直径的圆交于点M(异于点O),与过F且垂直于x轴的直线交于N,若S△OMF=4S△MNF,则双曲线C的离心率为 .C:x2a2-y2b2=1组卷:55引用:3难度:0.6 -
16.历史上第一个研究圆锥曲线的是梅纳库莫斯(公元前375年-325年),大约100年后,阿波罗尼斯更详尽、系统地研究了圆锥曲线,并且他还进一步研究了这些圆锥曲线的光学性质:如图甲,从椭圆的一个焦点出发的光线或声波,经椭圆反射后,反射光线经过椭圆的另一个焦点,其中法线l′表示与椭圆C的切线垂直且过相应切点的直线,如图乙,椭圆C的中心在坐标原点,焦点为F1(-c,0),F2(c,0)(c>0),由F1发出的光经椭圆两次反射后回到F1经过的路程为8c.利用椭圆的光学性质解决以下问题:
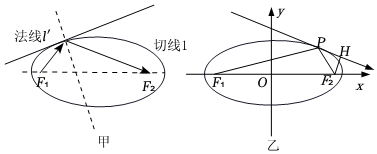
(1)椭圆C的离心率为 ;
(2)点P是椭圆C上除顶点外的任意一点,椭圆在点P处的切线为l,F2在l上的射影H在圆x2+y2=8上,则椭圆C的方程为 .组卷:235引用:7难度:0.5 -
17.已知半径为1的圆过点
,则该圆圆心到原点距离的最大值为 .(1,3)组卷:136引用:2难度:0.7 -
18.抛物线y2=ax的准线方程为x=
,则a=.12组卷:50引用:3难度:0.7 -
 19.如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,已知测得从D、C到库底与水坝的交线的距离分别为米、CB=10米,AB的长为10米,CD的长为DA=102米,则库底与水坝所成的二面角的大小为度.106组卷:76引用:2难度:0.5
19.如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,已知测得从D、C到库底与水坝的交线的距离分别为米、CB=10米,AB的长为10米,CD的长为DA=102米,则库底与水坝所成的二面角的大小为度.106组卷:76引用:2难度:0.5
三、解答题:本大题共5小题,共40分.解答应写出文字说明,证明过程或演算步骤.
-
20.设直线l的方程为(a+1)x+y-2-a=0.
(1)若直线l不经过第二象限,求实数a的取值范围;
(2)若直线l与x轴、y轴分别交于点M,N,且a>0,求△MON(O为坐标原点)面积的最小值及此时直线l的方程.组卷:333引用:3难度:0.7 -
 21.如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD满足AD∥BC,且AB=AD=AA1=2,BD=DC=2.2
21.如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD满足AD∥BC,且AB=AD=AA1=2,BD=DC=2.2
(Ⅰ)求证:AB⊥平面ADD1A1;
(Ⅱ)求直线AB与平面B1CD1所成角的正弦值.组卷:348引用:15难度:0.4 -
22.已知圆x2+y2-4ax+2ay+20a-20=0.
(1)求证:对任意实数a,该圆恒过一定点;
(2)若该圆与圆x2+y2=4外切,求a的值.组卷:442引用:4难度:0.3 -
 23.三棱柱ABC-A1B1C1中,M、N分别是A1B、B1C1上的点,且BM=2A1M,C1N=2B1N.设,AB=a,AC=b.AA1=c
23.三棱柱ABC-A1B1C1中,M、N分别是A1B、B1C1上的点,且BM=2A1M,C1N=2B1N.设,AB=a,AC=b.AA1=c
(Ⅰ)试用表示向量a,b,c;MN
(Ⅱ)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.组卷:3459引用:42难度:0.3 -
24.从椭圆
上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且x2a2+y2b2=1(a>b>0).AB=λOP(λ>0)
(1)求该椭圆的离心率.
(2)若该椭圆的准线方程是,求椭圆方程.x=±25组卷:46引用:4难度:0.1


