2021-2022学年湖北省武汉市洪山高级中学高二(上)月考数学试卷(12月份)
发布:2025/10/29 1:0:34
一、单项选择题:本大题共8小题,每小题5分,共40分.
-
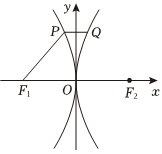 1.“米”是象形字.数学探究课上,某同学用抛物线C1:y2=-2px(p>0)和C2:y2=2px(p>0)构造了一个类似“米”字型的图案,如图所示,若抛物线C1,C2的焦点分别为F1,F2,点P在抛物线C1上,过点P作x轴的平行线交抛物线C2于点Q,若PF1=3PQ=6,则p=( )组卷:36引用:3难度:0.7
1.“米”是象形字.数学探究课上,某同学用抛物线C1:y2=-2px(p>0)和C2:y2=2px(p>0)构造了一个类似“米”字型的图案,如图所示,若抛物线C1,C2的焦点分别为F1,F2,点P在抛物线C1上,过点P作x轴的平行线交抛物线C2于点Q,若PF1=3PQ=6,则p=( )组卷:36引用:3难度:0.7 -
2.已知数列{an}是等差数列,Sn为数列的前n项和,且S2020>0,S2021<0,则( )
组卷:802引用:2难度:0.5 -
3.设{an}为等比数列,{bn}为等差数列,且b1=0,cn=an+bn,若数列{cn}是1,1,2,…,则{cn}的前10项和为( )
组卷:55引用:4难度:0.7 -
 4.如图,F1,F2分别是双曲线的左、右焦点,点P是双曲线与圆x2+y2=a2+b2在第二象限的一个交点,点Q在双曲线上,且x2a2-y2b2=1(a>0,b>0),则双曲线的离心率为( )F1P=12F2Q组卷:331引用:6难度:0.5
4.如图,F1,F2分别是双曲线的左、右焦点,点P是双曲线与圆x2+y2=a2+b2在第二象限的一个交点,点Q在双曲线上,且x2a2-y2b2=1(a>0,b>0),则双曲线的离心率为( )F1P=12F2Q组卷:331引用:6难度:0.5 -
5.已知椭圆mx2+
=1的焦距为2,则实数m=( )y22组卷:116引用:3难度:0.6 -
6.已知线段AB=4,其中点A,B分别在x轴与y轴正半轴上移动,若点A从(2
,0)移动到(2,0),则AB中点D经过的路程为( )3组卷:38引用:2难度:0.5 -
7.已知直线l1:(3+a)x+4y=5-3a,l2:2x+(5+a)y=8.若11∥l2平行,则a的值为( )
组卷:888引用:6难度:0.7 -
8.系统找不到该试题
二、多选题:本大题共4小题,每小题5分,共20分,少选得2分,多选得0分.
-
9.已知直线l:kx-y+k=0和圆O:x2+y2=4,则( )
组卷:217引用:7难度:0.5 -
10.下列说法正确的有( )
组卷:117引用:7难度:0.7 -
 11.如图所示圆台,O1,O2分别是上、下底面的圆心,母线AB与下底面所成的角为60°,BC为上底面直径,O2A=6,O1B=1,则( )组卷:75引用:3难度:0.5
11.如图所示圆台,O1,O2分别是上、下底面的圆心,母线AB与下底面所成的角为60°,BC为上底面直径,O2A=6,O1B=1,则( )组卷:75引用:3难度:0.5 -
12.P为椭圆C1:
=1上的动点,过P作C1切线交圆C2:x2+y2=12于M,N,过M,N作C2切线的两条切线,切线交于Q,则( )x24+y23组卷:119引用:3难度:0.5
三、填空题:本大题共4小题,每小题5分,共20分.
-
13.已知双曲线C的方程为:
,离心率为x2a2-y2b2=1(a>0,b>0),过C的右支上一点P(x0,y0),作两条渐近线的平行线,分别交x轴于M,N两点,且|OM|•|ON|=5.过点P作∠F1PF2的角平分线,F2在角平分线上的投影为点H,则|F1H|的最大值为 .355组卷:76引用:2难度:0.4 -
14.数列{an}的通项公式为an=(-1)n-1(4n-3),则它的前100项和S100=.
组卷:251引用:8难度:0.7 -
15.已知M(x1,y1),N(x2,y2)是圆C:(x-3)2+(y-4)2=4上的两个不同的点,若|MN|=2
,|x1+y1|+|x2+y2|的取值范围为 .2组卷:271引用:14难度:0.5 -
16.若直线l:x-2y+m=0与圆C:x2+y2-2y-4=0相切,则实数m=.
组卷:609引用:9难度:0.6
四、解答题:本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤
-
 17.如图,在△ABC中,AD是BC边上的高,以AD为折痕,将△ACD折至△APD的位置,使得PB⊥AB.
17.如图,在△ABC中,AD是BC边上的高,以AD为折痕,将△ACD折至△APD的位置,使得PB⊥AB.
(1)证明:PB⊥平面ABD;
(2)若AD=PB=4,BD=2,求二面角B-PA-D的正弦值.组卷:974引用:12难度:0.5 -
18.已知抛物线C:y2=2px(p>0)上的点M(5,m)到焦点F的距离为6.
(1)求抛物线C的方程
(2)过点P(2,-1)作直线l交抛物线C于A,B两点,且点P是线段AB的中点,求直线l方程.组卷:443引用:7难度:0.5 -
19.在数列{an}中,任意相邻两项为坐标的点P(an,an+1)均在直线y=2x+k上,数列{bn}满足条件:b1=2,bn=an+1-an(n∈N).
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)若cn=bnlog2,Sn=c1+c2+…+cn,求2n+1-Sn>60n+2成立的正整数n的最小值.1bn组卷:144引用:13难度:0.5 -
20.已知直线l:x-y-2=0和点A(-1,1),B(1,1).
(1)直线l上是否存在点C,使得△ABC为直角三角形,若存在,请求出C点的坐标;若不存在,请说明理由;
(2)在直线l上找一点P,使得∠APB最大,求出P点的坐标.组卷:328引用:3难度:0.5 -
21.已知实数x,y满足x2+y2=1,求
的取值范围.y+2x+1组卷:101引用:1难度:0.5 -
22.已知椭圆C:
+x2a2=1(a>b>0)经过点M(1,y2b2),N(22,0).2
(1)求椭圆C的方程;
(2)已知直线l的倾斜角为锐角,l与圆x2+y2=相切,与椭圆C交于A、B两点,且△AOB的面积为12,求直线l的方程.23组卷:266引用:3难度:0.6


