2022-2023学年广东省东莞市光明中学九年级（上）期中数学试卷

一．选择题（本大题共有10小题，每小题3分，共30分）

• 1．下列图形是汽车的标识，其中既是中心对称图形又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：238引用：6难度：0.9

  解析

• 2．若关于x的一元二次方程（k-1）x²+3x+k²-1=0的一个根为0，则k的值为（　　）

  A．0

  B．1

  C．-1

  D．1或-1
  组卷：888引用：10难度：0.7

  解析

• 3．将方程x²-6x+1=0配方后，原方程可变形为（　　）

  A．（x-3）2=8

  B．（x-3）2=-10

  C．（x+3）2=-10

  D．（x+3）2=8
  组卷：2101引用：30难度：0.6

  解析

• 4．关于抛物线y=

  5

  2

  （x+1）²-3的情况描述正确的是（　　）

  A．开口向上，对称轴是直线x=1，顶点坐标是（1，-3）

  B．开口向下，对称轴是直线x=-1，顶点坐标是（-1，3）

  C．开口向上，对称轴是直线x=-1，顶点坐标是（-1，-3）

  D．开口向下，对称轴是直线x=1，顶点坐标是（1，3）
  组卷：266引用：4难度：0.8

  解析

• 5．将抛物线y=3x²向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（　　）

  A．y=3（x+2）2+3	B．y=3（x-2）2+3
  C．y=3（x+3）2+2	D．y=3（x-3）2+2
  组卷：245引用：7难度：0.6

  解析

• 6．已知二次函数y=x²+3x-m（m为常数）的图象与x轴的一个公共点为（1，0），则关于x的一元二次方程x²+3x-m=0的两实数根是（　　）

  A．x1=1，x2=-4

  B．x1=1，x2=2

  C．x1=1，x2=-3

  D．x1=1，x2=3
  组卷：282引用：6难度：0.8

  解析

• 7．小颖初一时体重是30kg,到初三时体重增加到43.2kg,则她的体重平均每年增加的百分率为（　　）

  A．10%

  B．15%

  C．20%

  D．22%
  组卷：540引用：6难度：0.7

  解析

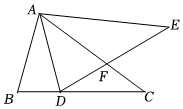• 8．如图，在△ABC中，AB＜AC，将△ABC以点A为中心逆时针旋转得到△ADE，点D在BC边上，DE交AC于点F．下列结论：①∠EAC=∠CAD；②DA平分∠BDE；③∠CDF=∠BAD，其中所有正确结论的序号是（　　）

  A．①②

  B．②③

  C．①③

  D．①②③
  组卷：335引用：2难度：0.6

  解析

五．解答题（三）（本大题共有2小题，每小题10分，共20分）

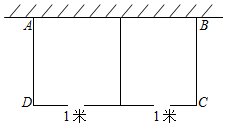• 24．如图，为了节约材料利用一面墙（墙长20米）用总长度43米的篱笆围成一个矩形鸡舍ABCD，中间用篱笆隔开，且留两个1米宽的小门，设篱笆BC长为x米．
  （1）用含x的代数式表示AB的长；
  （2）若矩形鸡舍ABCD面积为150平方米，求篱笆BC的长；
  （3）矩形鸡舍ABCD面积是否有可能达到210平方米？若有可能，求出相应x的值；若不可能，请说明理由．
  组卷：424引用：3难度：0.4

  解析

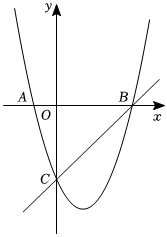• 25．如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（-1，0）、B（4，0）、C三点，且OB=OC，点P是抛物线上的一个动点．
  （1）求这个二次函数的解析式；
  （2）若点P在直线BC下方，P运动到什么位置时，四边形PBOC面积最大？求出此时点P的坐标和四边形PBOC的最大面积；
  （3）直线BC上是否存在一点Q，使得以点A、B、P、Q组成的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．
  组卷：748引用：6难度：0.1

  解析