当前位置：试卷中心 > 试卷详情

2023-2024学年重庆市七校高三（上）第一次月考数学试卷

发布：2024/9/8 11:0:12

一、单选题。（本大题共8小题，共40.0分。）

1．集合
A
=
{
x
∈
N
*
|
y
=
x
-
3
+
ln
（
6
-
x
）
}
的子集个数为（　　）
A．7 B．8 C．15 D．16
组卷：16引用：7难度：0.7
解析
2．命题“∃a∈[0.1]，a⁴+a²＞1”的否定是（　　）
A．∃a∉[0，1]，a⁴+a²＞1 B．∃a∈[0，1]，a⁴+a²≤1
C．∀a∈[0，1]，a⁴+a²＞1 D．∀a∈[0，1]，a⁴+a²≤1
组卷：472引用：22难度：0.8
解析
3．已知第二象限角α的终边过点P（-4，3），则
sinα
-
2
cosα
sinα
+
cosα
=（　　）
A．-11 B．
-
1
2
C．
-
5
7
D．1
组卷：245引用：3难度：0.8
解析
4．函数
f
（
x
）
=
e
x
-
1
e
x
+
1
•
cos
（
π
2
+
x
）
的部分图象大致形状是（　　）
A． B．
C． D．
组卷：26引用：1难度：0.8
解析
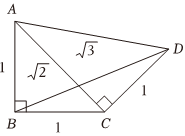5．古希腊数学家泰特托斯（Theaetetus,公元前417—公元前369年）详细地讨论了无理数的理论，他通过图来构造无理数
2
，
3
，
5
，…．如图，则cos∠BAD=（　　）
A．
2
6
-
3
3
6
B．
2
3
-
6
6
C．
2
3
+
6
6
D．
2
6
+
3
3
6
组卷：119引用：6难度：0.7
解析
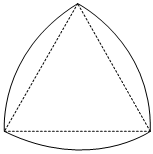6．“莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形，它在很多特殊领域发挥了超常的贡献值．“莱洛三角形”是分别以正三角形的顶点为圆心，以其边长为半径作圆弧，由这三段圆弧组成的曲边三角形（如图所示），现以边长为4的正三角形作一个“莱洛三角形”，则此“莱洛三角形”的面积为（　　）
A．
8
π
-
8
3
B．
8
π
-
12
3
C．
16
π
-
8
3
D．
16
π
-
4
3
组卷：18引用：5难度：0.6
解析
7．定义在R上的偶函数f（x）满足f（x）=f（4-x），当x∈[0，2]时，
f
（
x
）
=
（
e
）
x
，若在区间x∈[0，10]内，函数g（x）=f（x）-mx-1，（m＞0）有5个零点，则实数m的取值范围是（　　）
A．
（
0
，
e
5
-
1
10
）
B．
（
0
，
e
-
1
10
]
C．
（
e
-
1
11
，
e
-
1
6
）
D．
[
α
-
1
10
，
a
-
1
6
）
组卷：35引用：2难度：0.4
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题。（本大题共6小题，共70.0分。）

21．近日，随着李佳琦直播事件的持续发酵，国货品牌上演花式直播．现有一品牌商也想借这个热度，采取了“量大价优”“广告促销”等方法，提高其下某商品的销售额．市场调查发现，这种商品供不应求，生产出来都能销售完．且此商品的月销售量m（万件）与广告促销费用x（万元）（x＞0）满足：
m
=
12
-
18
2
x
+
1
，该产品的单价n与销售量之间的关系定为：
（
n
=
9
+
9
m
）
万元，已知生产一万件该产品的成本为8万元，设该产品的利润为y万元．
（1）求y与x的函数关系式；（利润=销售额-成本-广告促销费用）
（2）当广告促销费用定为多少万元的时候，该产品的利润最大？最大利润为多少万元？
组卷：15引用：2难度：0.6
解析
22．设a＞0且a≠1，
f
（
x
）
=
1
+
lo
g
a
x
lo
g
a
（
x
+
1
）
．
（1）若a=2，求y=f（x）在x=1处的切线方程；
（2）若f（x）存在极值点x₀．
①求a的取值范围；
②证明x₀+f（x₀）≥3．
组卷：25引用：2难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．∃a∉[0，1]，a⁴+a²＞1	B．∃a∈[0，1]，a⁴+a²≤1
C．∀a∈[0，1]，a⁴+a²＞1	D．∀a∈[0，1]，a⁴+a²≤1

A．（ 0 ， e 5 - 1 10 ）	B．（ 0 ， e - 1 10 ]
C．（ e - 1 11 ， e - 1 6 ）	D． [ α - 1 10 ， a - 1 6 ）

2023-2024学年重庆市七校高三（上）第一次月考数学试卷

一、单选题。（本大题共8小题，共40.0分。）

1．集合A={x∈N*|y=x-3+ln（6-x）}的子集个数为（ ）

2．命题“∃a∈[0.1]，a4+a2＞1”的否定是（ ）

3．已知第二象限角α的终边过点P（-4，3），则sinα-2cosαsinα+cosα=（ ）

4．函数f（x）=ex-1ex+1•cos（π2+x）的部分图象大致形状是（ ）

5．古希腊数学家泰特托斯（Theaetetus,公元前417—公元前369年）详细地讨论了无理数的理论，他通过图来构造无理数2，3，5，…．如图，则cos∠BAD=（ ）

7．定义在R上的偶函数f（x）满足f（x）=f（4-x），当x∈[0，2]时，f（x）=（e）x，若在区间x∈[0，10]内，函数g（x）=f（x）-mx-1，（m＞0）有5个零点，则实数m的取值范围是（ ）

四、解答题。（本大题共6小题，共70.0分。）

22．设a＞0且a≠1，f（x）=1+logaxloga（x+1）．（1）若a=2，求y=f（x）在x=1处的切线方程；（2）若f（x）存在极值点x0．①求a的取值范围；②证明x0+f（x0）≥3．

1．集合
A
=
{
x
∈
N
*
|
y
=
x
-
3
+
ln
（
6
-
x
）
}
的子集个数为（　　）

2．命题“∃a∈[0.1]，a⁴+a²＞1”的否定是（　　）

3．已知第二象限角α的终边过点P（-4，3），则
sinα
-
2
cosα
sinα
+
cosα
=（　　）

4．函数
f
（
x
）
=
e
x
-
1
e
x
+
1
•
cos
（
π
2
+
x
）
的部分图象大致形状是（　　）

5．古希腊数学家泰特托斯（Theaetetus,公元前417—公元前369年）详细地讨论了无理数的理论，他通过图来构造无理数
2
，
3
，
5
，…．如图，则cos∠BAD=（　　）

7．定义在R上的偶函数f（x）满足f（x）=f（4-x），当x∈[0，2]时，
f
（
x
）
=
（
e
）
x
，若在区间x∈[0，10]内，函数g（x）=f（x）-mx-1，（m＞0）有5个零点，则实数m的取值范围是（　　）

22．设a＞0且a≠1，
f
（
x
）
=
1
+
lo
g
a
x
lo
g
a
（
x
+
1
）
．
（1）若a=2，求y=f（x）在x=1处的切线方程；
（2）若f（x）存在极值点x₀．
①求a的取值范围；
②证明x₀+f（x₀）≥3．