2022-2023学年天津一中高一（下）期末数学试卷

一、选择题：（每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知（1-i）²z=3+2i,则z=（　　）

  A．-1- 3 2 i

  B．-1+ 3 2 i

  C．- 3 2 +i

  D．- 3 2 -i
  组卷：4469引用：32难度：0.8

  解析

• 2．已知向量

  a

  =

  （

  1

  ，-

  1

  ）

  ，

  b

  =

  （

  2

  ，

  1

  ）

  ，

  c

  =

  （

  2

  ，

  λ

  ）

  ．若

  c

  ∥

  （

  2

  a

  +

  b

  ）

  ，则λ=（　　）

  A． - 1 2

  B．0

  C． 1 2

  D．8
  组卷：304引用：5难度：0.7

  解析

• 3．已知α，β，γ是三个两两不重合的平面，m,n是两条不重合的直线，则下列命题：
  ①若m⊂α，n⊂α，m∥β，n∥β，则α∥β；②若m⊥α，n⊥β，α∥β，则m∥n；
  ③若m∥α，m⊂β，a∩β=n,则m∥n；④若α⊥γ，β⊥γ，α∩β=m,则m⊥γ．
  其中所有正确命题的编号是（　　）

  A．①②③④

  B．②③④

  C．②④

  D．③④
  组卷：105引用：2难度：0.8

  解析

• 4．在5件产品中，有3件一级品和2件二级品，从中任取2件，下列事件中概率为

  7

  10

  的是（　　）

  A．都是一级品	B．都是二级品
  C．一级品和二级品各1件	D．至少有1件二级品
  组卷：135引用：6难度：0.7

  解析

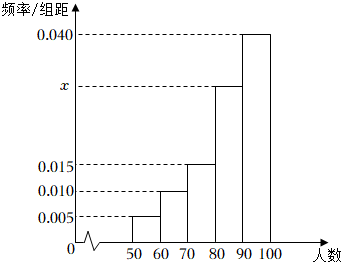• 5．某校随机抽取了400名学生进行成绩统计，发现抽取的学生的成绩都在50分至100分之间，进行适当分组画出频率分布直方图如图所示，下列说法正确的是（　　）

  A．直方图中x的值为0.040

  B．在被抽取的学生中，成绩在区间[70，80）的学生数为30人

  C．估计全校学生的平均成绩为84分

  D．估计全校学生成绩的样本数据的80%分位数约为93分
  组卷：1055引用：6难度：0.8

  解析

• 6．高一年级某同学参加了学校“数学社”“物理社”“话剧社”三个社团的选拔，该同学能否成功进入这三个社团是相互独立的．假设该同学能够进入“数学社”“物理社”“话剧社”三个社团的概率分别为m,n,

  1

  5

  ，该同学进入两个社团的概率为

  3

  20

  ，且三个社团都进不了的概率为

  2

  5

  ，则m+n=（　　）

  A． 7 12

  B． 1 12

  C． 8 15

  D． 9 20
  组卷：247引用：2难度：0.8

  解析

三、解答题：（本大题共4小题共46分。解答应写出文字说明，证明过程或演算步骤。）

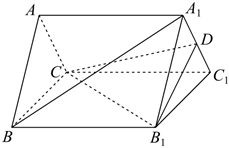• 19．如图，在正三棱柱ABC-A₁B₁C₁中，已知AB=AA₁=3，且D为A₁C₁的中点．
  （1）求证：A₁B∥平面B₁CD；
  （2）求A₁B与平面BCC₁B₁所成角的余弦值．
  组卷：556引用：2难度：0.6

  解析

• 20．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，其中AD∥BC，AB⊥AD，PA=4，AB=AD=

  1

  2

  BC=2，E为棱BC上的点，且BE=

  1

  4

  BC．
  （Ⅰ）求证：DE⊥平面PAC；
  （Ⅱ）求平面APC与平面PCD夹角的余弦值；
  （Ⅲ）求点E到平面PCD的距离．
  组卷：394引用：4难度：0.5

  解析