2022-2023学年重庆市忠县后乡三校八年级（下）期中数学试卷

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.

• 1．2的相反数是（　　）

  A． 1 2

  B．- 1 2

  C．2

  D．-2
  组卷：780引用：90难度：0.9

  解析

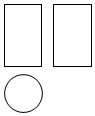• 2．如图是一个几何体的三视图，该几何体是（　　）

  A．球

  B．圆锥

  C．圆柱

  D．棱柱
  组卷：973引用：13难度：0.8

  解析

• 3．已知a＞b,下列不等式的变形不正确的是（　　）

  A．a-1＞b-1

  B．a-c＞b-c

  C．2a＞2b

  D．ac＞bc
  组卷：328引用：7难度：0.8

  解析

• 4．三角形的三边分别为a、b、c,由下列条件不能判断它是直角三角形的是（　　）

  A．a：b：c=13：5：12	B．a= 1 3 ，b= 1 4 ，c= 1 5
  C．a2=（b+c）（b-c）	D．a2-b2=c2
  组卷：203引用：1难度：0.8

  解析

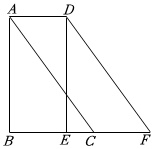• 5．如图，在Rt△ABC中，∠B=90°，AB=4，将Rt△ABC沿BC向右平移得到△DEF，若四边形ACFD的面积等于8，则平移的距离等于（　　）

  A．2

  B．3

  C． 2 3

  D．4
  组卷：182引用：2难度：0.7

  解析

• 6．按如图所示的运算程序，能使输出的结果为4的是（　　）
  

  A．x=1，y=2

  B．x=2，y=1

  C．x=3，y=1

  D．x=2，y=3
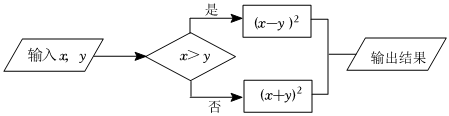  组卷：207引用：6难度：0.7

  解析

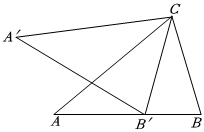• 7．如图，将△ABC绕点C顺时针旋转后得到△A′B′C，且点B′恰好落在边AB上，若∠B=α，则∠A′CA=（　　）

  A． 1 2 α

  B．α

  C．90°-α

  D．180°-2α
  组卷：320引用：2难度：0.5

  解析

• 8．将一些完全相同的梅花按如图所示的规律摆放，第1个图形有5朵梅花，第2个图形有8朵梅花，第3个图形有13朵梅花，⋯，按此规律，则第6个图形中共有梅花的朵数是（　　）
  

  A．39

  B．40

  C．41

  D．42
  组卷：46引用：2难度：0.6

  解析

三、解答题：（本大题8个小题，19题8分，20-26每小题8分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.

• 25．如图，抛物线y=-x²+bx+c与x轴交于点A（-3，0），点B（1，0），与y轴相交于点C．
  （1）求抛物线的函数表达式；
  （2）点P是第二象限内抛物线上一动点，连接AC，D是线段AC的中点，连接AP，DP，求△APD面积的最大值及此时点P的坐标；
  （3）在（2）中，△APD面积的取最大值的条件下，将原抛物线沿射线AC的方向平移2

  2

  个单位长度，得到新抛物线y₁．点M为新抛物线y₁对称轴上一点，点N为平面内一点，若以A，P，M，N为顶点的四边形是矩形，直接写出所有符合条件的点N的坐标，并选择其中一个写出求解过程．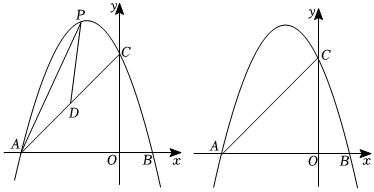
  
  组卷：415引用：2难度：0.1

  解析

• 26．如图1，△ABC中，AC=BC，点D是线段AC上任意一点，连接BD．
  （1）如图1，若∠ACB=90°，过点C作CE⊥BD于点E，连接AE，若AD：CD=3：2，CE=2，求AE．
  （2）如图2，点E在线段BC上，连接AE，点F在线段AE上，点G是线段DB的中点，连接DF，FG．若∠ACB=∠EFD，∠AEB=3∠FAD，求证：FG⊥CG．
  （3）如图3，若∠CDB=60°，点N是射线DB上的动点，点M是射线DC上的动点，点P是平面上任意一点，连接PM，PN，MN，PM=PN，且∠MPN=120°，当线段DP的距离最大时，连接AP，AN，若∠NAM=45°，线段MN的长为4，直接写出△PAN的面积．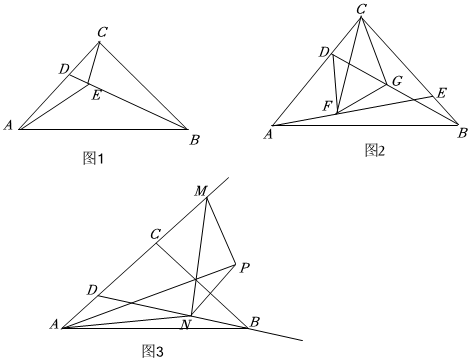
  
  组卷：221引用：1难度：0.1

  解析