当前位置：试卷中心 > 试卷详情

2023-2024学年浙江省杭州市四校高二（上）联考数学试卷（10月份）

发布：2024/9/8 0:0:9

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求.

1．直线
3
x
+
y
-
1
=
0
的斜率与y轴上的截距分别为（　　）
A．
3
，
1
B．
-
3
，
1
C．
3
，-
1
D．
-
3
，-
1
组卷：124引用：2难度：0.8
解析
2．如果一个复数的实部与虚部相等，则称这个复数为“等部复数”，若复数z=（2-ai）i为“等部复数”，则实数a的值为（　　）
A．-1 B．1 C．2 D．-2
组卷：108引用：12难度：0.8
解析
3．平面α，β互相平行的一个充分条件是（　　）
A．α，β都垂直于同一平面
B．某一直线与α，β所成角相等
C．α，β都平行于同一直线
D．α，β都垂直于同一直线
组卷：49引用：2难度：0.5
解析
4．已知直三棱柱ABC-A₁B₁C₁，∠BAC=90°，AB=AC=
1
2
A
A
1
，那么异面直线B₁C与A₁B所成角的余弦值为（　　）
A．
30
10
B．
1
2
C．
15
5
D．
10
10
组卷：93引用：8难度：0.7
解析
5．设非零向量
a
和
b
的夹角为θ，定义运算：
|
a
×
b
|
=
|
a
|
|
b
|
sinθ
．已知
a
=
（
1
，
1
）
，
b
=
（
-
1
，
2
）
，则
|
a
×
b
|
=（　　）
A．2 B．
7
C．3 D．
10
组卷：57引用：2难度：0.5
解析
6．点P（x,y）在圆x²+y²=1上运动，则|4x-3y+4|的取值范围（　　）
A．[0，1] B．[0，9] C．[1，8] D．[1，9]
组卷：167引用：2难度：0.6
解析
7．在△ABC中，A（-1，0），B（0，1），点C在直线y=x上运动，则△ABC内切圆的半径的最大值是（　　）
A．
3
-
2
2
B．
2
6
C．
2
-
1
D．
1
-
2
2
组卷：50引用：1难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．设抛物线y=x²-3与两坐标轴的交点分别记为M，N，G，曲线C是经过这三点的圆．
（1）求圆C的方程．
（2）过P（-1，0）作直线l与圆C相交于A，B两点，
（i）用坐标法证明：|PA|•|PB|是定值．
（ii）设Q（0，-2），求|QA|²+|QB|²的最大值．
组卷：113引用：4难度：0.3
解析
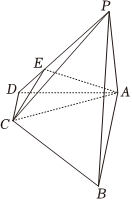22．如图，四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠BAD=∠ACB=90°，AB=
3
AC=3CD=6，PA⊥BC，在锐角三角形PAC中，PC=4．
（Ⅰ）点E满足
PE
=
λ
PD
，试确定λ的值，使得直线PB∥平面ACE，并说明理由．
（Ⅱ）当PA的长为何值时，直线AD与平面PBC所成的角的正弦值为
2
3
．
组卷：35引用：1难度：0.6
解析